| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
ENVELOPE SURFACE OF A FAMILY OF SURFACES
1) Case of a family of surfaces with one parameter.
If 
is defined by the Cartesian equation (1): f(x,
y,
z,
t)
= 0, then the equation of the envelope is obtained by eliminating
t
between (1) and the equation (2):  .
If 
is parametrically defined by (M(u,v,t))u,v
,
then solving 
gives, by elimination of one of the parameters u,v,t, the parametrization
of the envelope.
If |
The envelope of a family of surfaces with one parameter
is the surface 
union of the characteristic curves 
of the surfaces 
,
limit curves when 
goes to t of the intersection curves between
and 
; the
surface 
is tangent at any of its points to a surface
and "in general", any surface
is tangent along a curve to 
;
the restrictive cases are the following ones:
- on an interval, the surfaces
pass by a fixed curve, in which case, this curve belongs to the envelope.
- the surfaces do not intersect with
one another (for example, concentric spheres, or surfaces for which the
intersection points are imaginary).
The family of characteristic curves
then has, in general, an envelope,
which is the cuspidal edge
of the surface .
With the above notations in the parametric case, since
the condition
is symmetrical in u,v and t, the two envelopes of the surfaces
loci of the points (M(u,v,t))u,t
and the surfaces 
loci of the points (M(u,v,t))v,t
are the same as those of the surfaces ;
the common envelope is in fact the locus of the points where the surfaces
of the three families are tangent along a line.
When the surfaces
are planes, the characteristic curve is a line that remains tangent to
the cuspidal edge of the envelope
(which then is a ruled developable
surface).
Examples:
- the polar
developable of a curve is the envelope of its normal planes.
- the Dupin
cyclides and the tubes are envelopes
of spheres.
2) Case of a family with two parameters.
If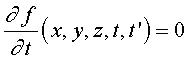 
is defined by the Cartesian equation (1): f(x,
y,
z,
t,
t') = 0, then the equation of the envelope can be obtained by eliminating
t and t' between (1) , (2): 
and (3):  .
If 
is defined parametrically by (M(u,v,t, t'))u,v
,
then solving  ???
(condition for these 4 vectors to be coplanar) gives, by elimination of
two of the parameters u,v,t,t', the parametrization of the envelope. |
The envelope of a family of surfaces with two parameters 
is the surface
generated by the characteristic points of the surfaces 
,
limit points when (t1 ,t'1)
goes to (t ,t') of the intersections between 
and 
???;
the surface
is tangent at any of its points to a surface
and "in general", every surface
is tangent at at least one point to .
With the above notations in the parametric case, since
the condition
is symmetrical in u,v,t,t' , then envelope of the
is also the envelope of 3 other families with two parameters: the common
envelope is in fact the locus of the points where the surfaces of the 4
families are tangent.
Examples:
- Every surface is the envelope of its tangent
planes.
- The parallel
surfaces of a surface are the envelopes of spheres with constant radius
centered on this surface.
- The pedal
of a surface
with respect to a point O is the envelope of the spheres with diameter
[OM] when M describes .
- The (reciprocal)
polar of a surface
with respect to a sphere (S) is the envelope of the polar planes
with respect to (S) of the points of .
- The envelope of the plane of a triangle [ABC]
the vertices of which move on the axes Ox, Oy et Oz is
- an
astroidal
surface: 
when the distance from the center of gravity to O is constant
- the cubic
surface: xyz = a3 when the tetrahedron
OABC
keeps a constant volume
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017
and with normal vector 
,
then the envelope is the ruled surface union of the lines passing by 
.