For an initial surface (S0) with current point , a parallel is a set (Sa) of points .

Two surfaces are said to be parallel if any normal to one is normal to the other; it can be proved that, then, the distance between two points with common normal is a constant, called parallelism constant. Do not mistake this notion for the notion of translated surface.

Like for planes, the parallelism relation of surfaces is an equivalence relation.

The parallel surfaces of a surface (S₀) are the surfaces (S_a), parallel of index a of (S₀), obtained by algebraically marking a "length" a from the points on (S₀) on the oriented normal, in other words, it is the locus of the points M =    where is the normal vector at M₀. Since the parallelism relation is symmetric, (S₀) is also parallel to (S_a).

The union of (S_a) and (S_-a) is the envelope of the spheres with radius a centered on (S₀).

The singular points of the parallel surfaces describe the focal of the base surface????
 

A similar notion is that of level surface of the function "distance (of a point in space) to the surface". These level surfaces are composed of portions of parallel surfaces and portions of spheres, and one of their interests is that they constitute a partition of space, contrary to the parallel surfaces.
 
 

Opposite, animation obtained by the succession of various parallel surfaces of a Moebius strip. The parallel surface of index a is identical to that of index -a, contrary to the parallel surfaces of a normal strip.... Moreover, this surface has the feature of being strictly parallel to itself.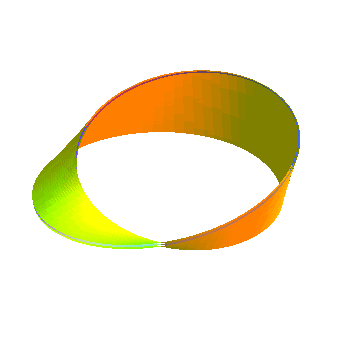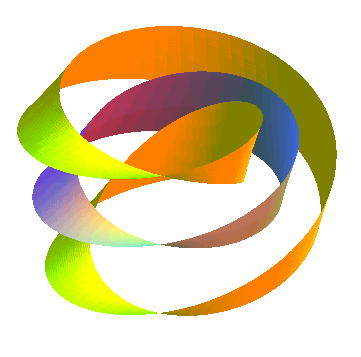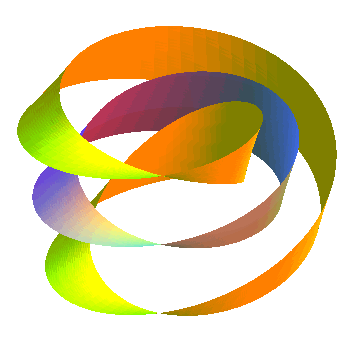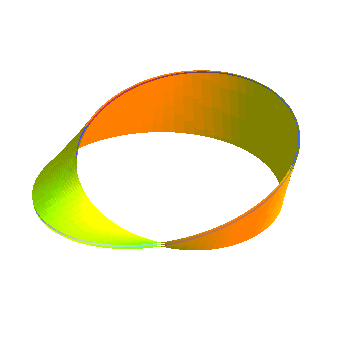

 
 

next surface

previous surface

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2017