Steven Anson Coons (1912-1979): American computer engineer.

 

Given four arcs parametrized on [0,1]  such that  The Coons patch is the surface parametrized by  where ,  and  so that .

The Coons patch provides a method to construct a surface supported on a given contour, when the latter is composed of 4 arcs of curves.

Examples:

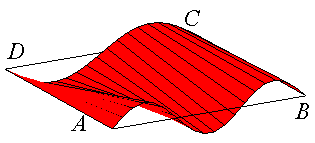
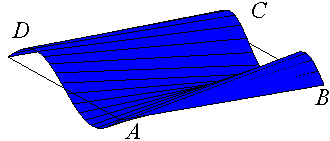
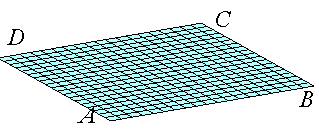
First ruled surface parametrized by M1   joining points P1(t) to  points Q1(t).	Second ruled surface parametrized by M2 joining points P2(u) to points Q2(u).	Bilinear patch parametrized by M3 , portion of hyperbolic paraboloid  lying on the quadrilateral ABCD. The patch is flat if the 4 vertices are coplanar.	Final Coons patch  M1 + M2 - M3
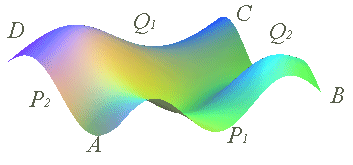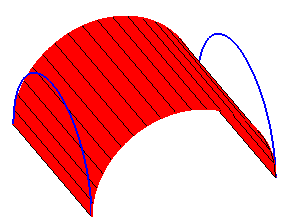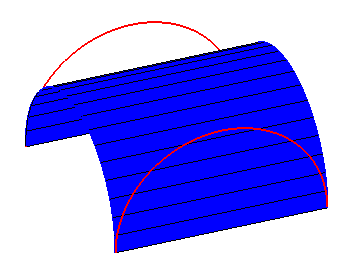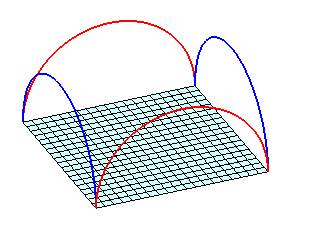
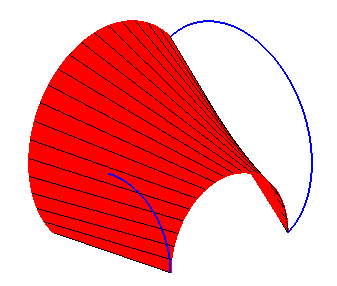
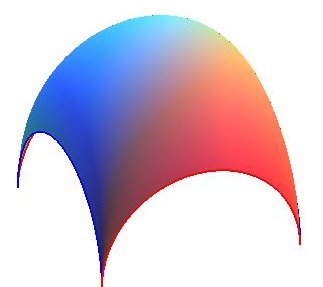
		Edge formed by 4 arcs of circles of the same radius	We get a Bohemian dome

 
 
 

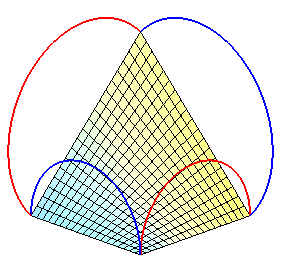
Production of a sphere thanks to Coons patches

Egg made by assembling Coons patches made by Alexandre Demir, for the best worker in France prize.

See also the Bezier surfaces.
 

next surface

previous surface

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2017