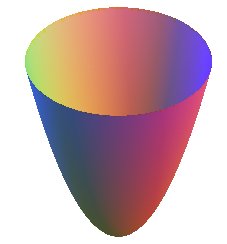
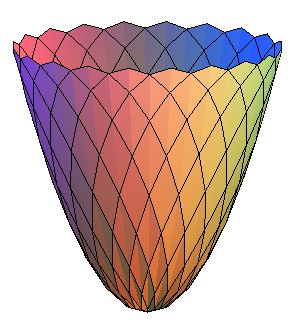
Paraboloid of revolution

PARABOLOID OF REVOLUTION

The paraboloid of revolution is the surface obtained by the revolution of a parabola around its axis.

Cylindrical equation: .
Cartesian equation: .
Quadric.
Cartesian parametrizations :

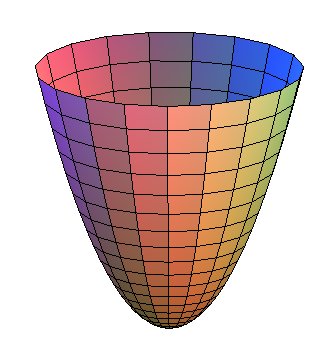
where coordinates lines are parallel circles and meridian parabolas :
(). where coordinates lines are parabolas :
other parabolas :
ellipses :

First fundamental quadratic form: .
Surface element: .
Second fundamental quadratic form: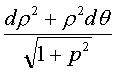
Total curvature:
All the points are elliptic and there is an umbilic: the vertex O.

Volume of the paraboloidic bowl with height h, the radius of the circle at the summit being R (): (half of the circumscribed cylinder).
Area of this bowl: ; approximation for a small h : .

Remarkable curves traced on the paraboloid of revolution:
- the curvature lines are the parallels (circles) and the meridians (parabolas),
- there are no asymptotic lines,
- the geodesics are the curves solution of: ,
- the helices.

- the 3D basins.

A paraboloid of revolution can be physically obtained by rotating a liquid at constant speed around an axis.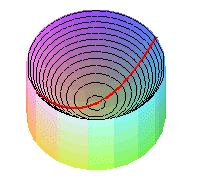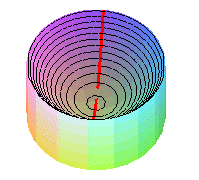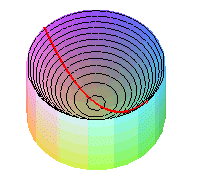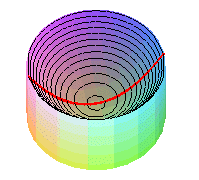

See, more generally, elliptic paraboloids.

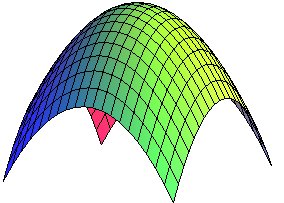
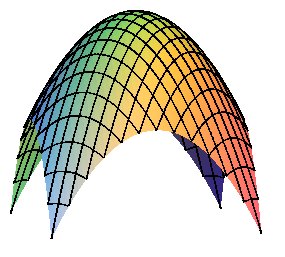
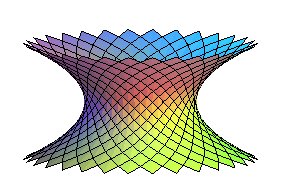
The parabola can also be rotated around a line perpendicular to its axis.
We obtain a surface that looks like a hyperboloid of revolution, but which is of degree 4.
Cylindrical equation: , cartesian equation: .
Cartesian parameterization:.
Area for : .

Solar oven of Odeillo in the Pyrenees.
See the principle at parabola.
Parabolic antenna

next surface previous surface 2D curves 3D curves surfaces fractals polyhedra

where coordinates lines are parallel circles and meridian parabolas : ().	where coordinates lines are parabolas :	other parabolas :	ellipses :

First fundamental quadratic form: . Surface element: . Second fundamental quadratic form: Total curvature: All the points are elliptic and there is an umbilic: the vertex O.
Volume of the paraboloidic bowl with height h, the radius of the circle at the summit being R (): (half of the circumscribed cylinder). Area of this bowl: ; approximation for a small h : .