FOLIUM
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
FOLIUM

| Curve studied by Longchamps in 1884, Brocard in 1887.
From the Latin folium: "leaf". |
| Polar equation: Cartesian equation: Rational quartic. |
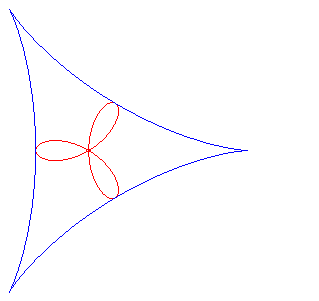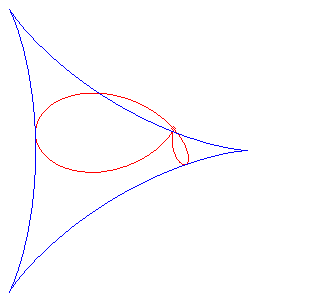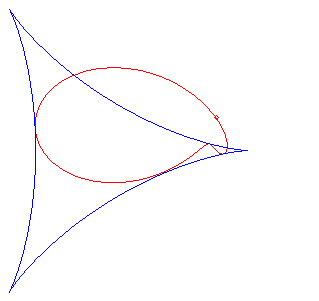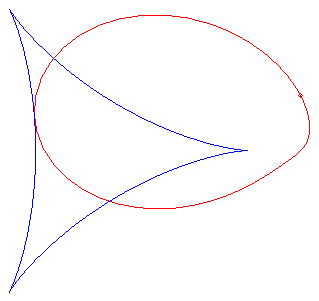
The folia are the pedals of the deltoid; here, the point O is the pole of the pedal, and the centre of the deltoid is A(a, b) and its cuspidal point is B(a – 3r, b); r is the radius of the inscribed circle of the deltoid, which is parametrized by: 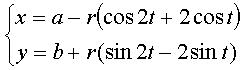
When the pole of the pedal is located on the deltoid, we get the bifolia; more precisely, if we take we get the bifolium:
.
When the pole of the pedal is located inside the deltoid, we get the trifolia.
For b = 0 (case where the pole of the pedal is located on the axis of the deltoid), the folium is said to be right (it is then symmetrical about Ox), otherwise it is oblique.
Special cases of right folia:
a = – r (pole of the pedal at a vertex of the deltoid): regular bifolium.
a = 0 (pole of the pedal at the centre of the deltoid): regular trifolium (rose with three petals).
a = r: torpedo (polar equation ).
a = 3r (the pole of the pedal is on a cuspidal point of the deltoid): simple folium.
For , the folium assumes a nice shape of an egg:
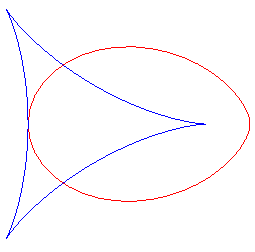
See also the beetles, that are to the astroid what the folia are to the deltoid.
The Cartesian folia, the parabolic folia, and the Dürer folia are not folia in the sense of this page.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017