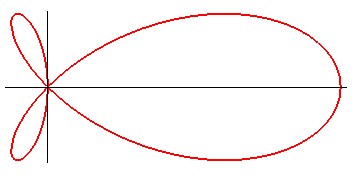
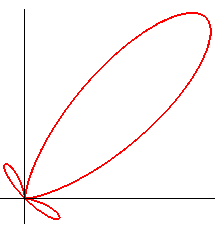
TORPEDO CURVE

| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
TORPEDO CURVE

| Curve studied by G. Gohierre de Longchamps in 1884 (geometrie
analytique, tome 2, 511-515).
Homemade name (G. de Longchamps called this curve the right trifolium, but this name now refers to a more general family). |
 |
Polar equation: Cartesian equation: Cartesian parametrization: Complex parametrization: Rational quartic. In a frame turned by p/4:
|
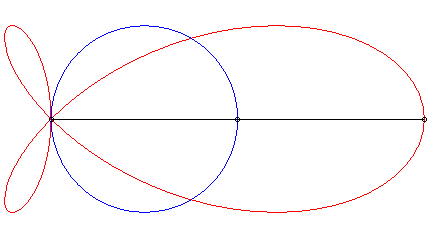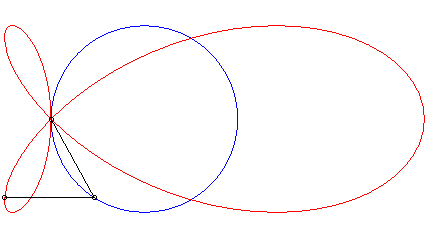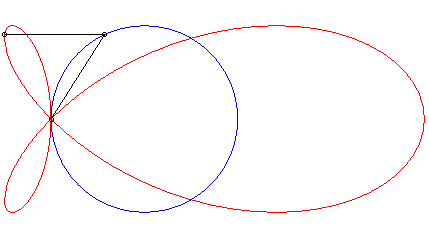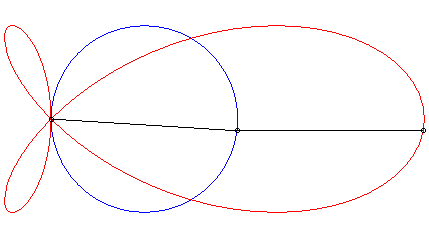
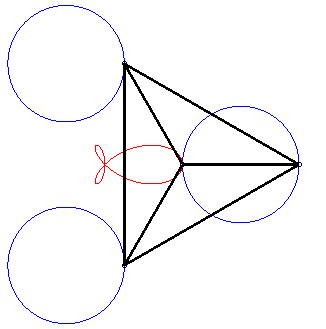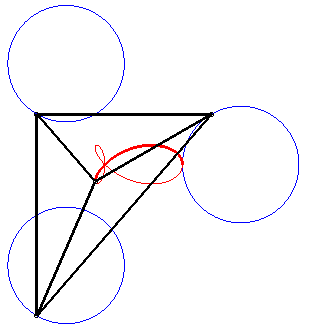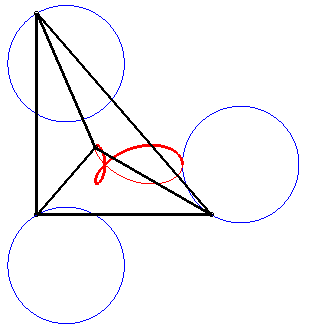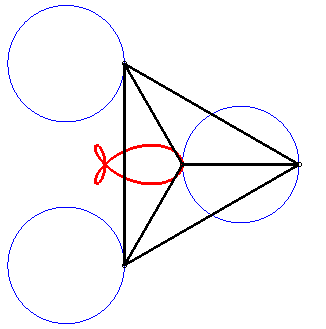
| The torpedo is the strophoid
of a circle (here the circle with centre (a/4, 0) passing by O)
with respect to a point O on the circle and a point A located
at infinity in the direction of the diameter passing by O.
|
 |
|
It is also a special case of right trifolium (pedal of a deltoid with respect to the point on the inscribed circle that is the symmetric image of the vertex of the deltoid - see folium), of "fish curve" and of tritrochoid (cf the complex parametrization). It is the locus of the isobarycentre of 3 circular motions with same radius, two of which have opposite speeds while the other has double speed. |
 |
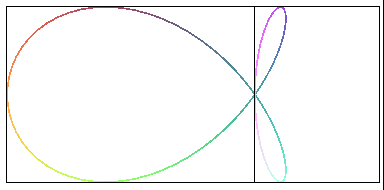
| Like all "fish" curves, the torpedo is a planar projection of Viviani's window. |
 |
It can also be obtained as the orthopolar of a circle.
See equilateral trefoil for a succinct study of its inverse.
A very close variation of the torpedo is called the "Cramer
trifolium":
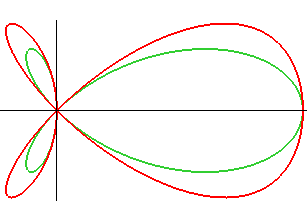 |
Cartesian equation: Polar equation: |
Who knows why certain mathematicians studied variations
of the torpedo and called them "dickoids":
|
|
|
Tardy dickoid |
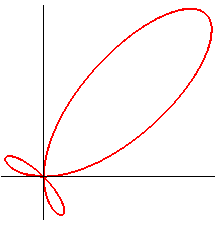 |
 |
 |

| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017