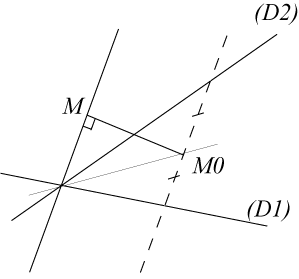
When the point
In the following, we take the orthogonal lines
Therefore, we have the simple result in polar coordinates:
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
ORTHOPOLAR OF A CURVE WITH RESPECT TO TWO LINES
| Notion studied by Henri Lazennec in 2015.
Homemade name. |
| Given two secant lines When the point In the following, we take the orthogonal lines Therefore, we have the simple result in polar coordinates: |
 |
| The orthopolar with respect to the axes of the curve |
Examples (initial curve in blue, orthopolar in red):
| The orthopolars of lines that do not pass by O are the strophoids.
More precisely, the orthopolar with respect to the axes of the line |
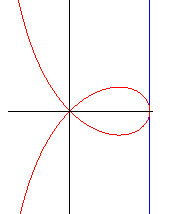 |
| The orthopolar of a circle centred on O is a quadrifolium. |
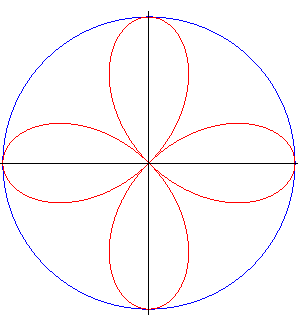 |
| The orthopolar with respect to the axes of the circle passing by O For |
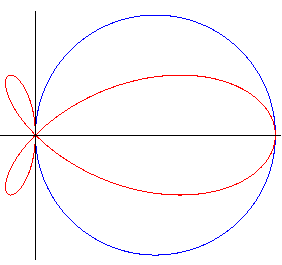 |
| ... and for |
 |
| An example with a circle that does not pass through O. |
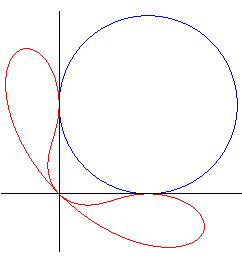 |
| The orthopolar of the cross-curve |
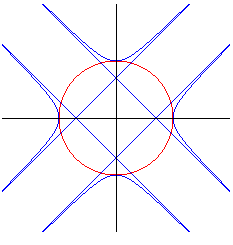 |
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017