TRISECTRICE ET SECTRICE DE CEVA
Ceva
trisectrix and sectrix, Cevasche Trisektrix und Sektrix
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
TRISECTRICE ET SECTRICE DE CEVA
Ceva
trisectrix and sectrix, Cevasche Trisektrix und Sektrix
| Courbe étudiée par Ceva en 1699.
Giovanni Ceva (1648-1734) : mathématicien et ingénieur italien. |
Équation polaire :  .
Paramétrisation cartésienne :  .
Parmétrisation complexe :  .
Équation cartésienne :  .
Sextique rationnelle. |
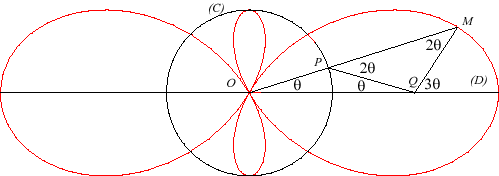
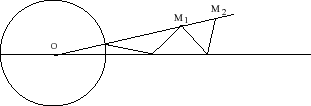
| Un cercle (C) de centre O et de rayon a
et une droite (D) passant par O ((D) est ici Ox)
étant donnés, la trisectrice de Céva est le lieu du
point M tels que OP = PQ = QM avec P
sur (C), Q sur (D) et tels que O, P
et M sont alignés.
L'angle xOM est le tiers de l'angle xQM , d'où le nom de trisectrice. Comparer avec la construction de la trisectrice de Maclaurin. |
 |
| L'expression complexe ,
équivalente à la construction précédente, montre
que la trisectrice de Ceva est une polytrochoïde,
composée de 3 mouvements circulaires uniformes. |
 |
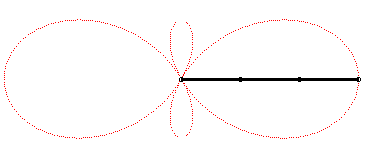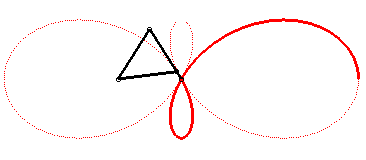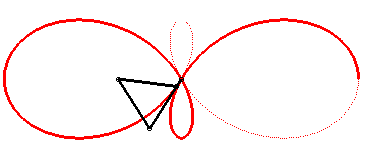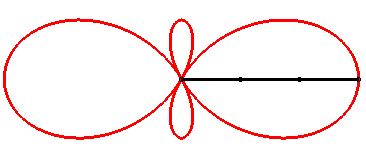| Comme toute tritrochoïde, la trisectrice de Ceva est le lieu du centre de gravité de 3 mouvements circulaires. |
 |
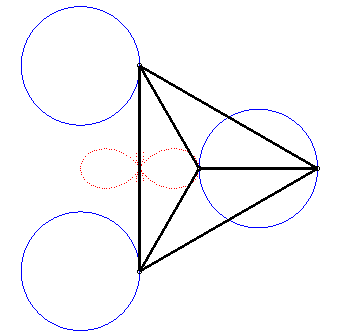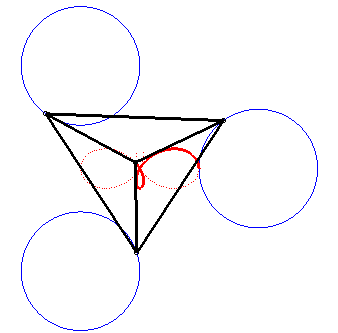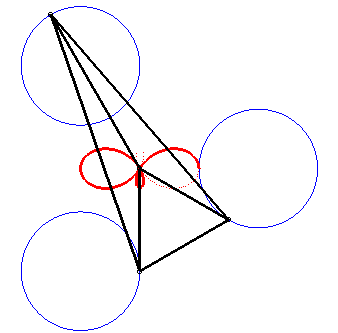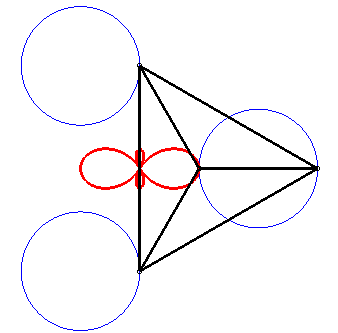Cette courbe est aussi une conchoïde
du trèfle à 4 feuilles
(elle rentre donc dans la famille des conchoïdes
de rosaces).
La construction ci-dessus peut se poursuivre, ainsi que le montre la figure :
La courbe d'ordre n, d'équation polaire 
est une (2n+1)-sectrice,
et désignée comme "sectrice de Ceva". |
|
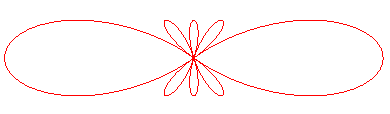
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2020