PARABOLE (CUBIQUE) GAUCHE
Skew (cubic) parabola (or twisted cubic), schiefe (kubische)
Parabel
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
PARABOLE (CUBIQUE) GAUCHE
Skew (cubic) parabola (or twisted cubic), schiefe (kubische)
Parabel
| Nom donné par Seydewitz en 1847. |
Système d’équations cartésiennes
:  .
Paramétrisation cartésienne :  .
|
La parabole (cubique) gauche est la courbe de paramétrisation
ci-dessus.
| Son nom vient de ce que ses projections sur les plans xOy, xOz et yOz sont respectivement une parabole, une parabole cubique, et une parabole semi-cubique. |
 |
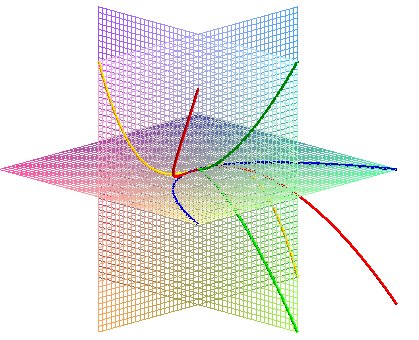Elle est l'intersection des trois quadriques:
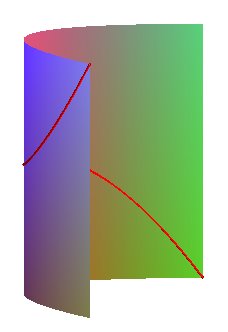
(cylindre parabolique),
(paraboloïde hyperbolique),
et 
(cône de révolution). |
intersection du cylindre et du paraboloïde (qui ont en commun également la droite de l'infini du plan x = 0) |
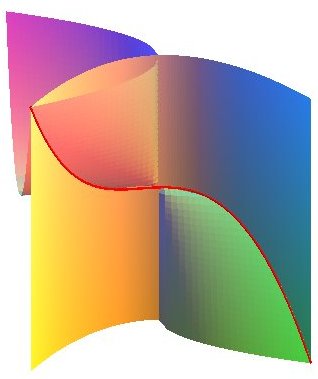
intersection du cylindre et du cône (qui ont en commun également la droite Oz) |
vue des 3 quadriques (Alain Esculier) |
| Sa projection sur le plan y + z = 0 est, à
dilatation près, une cubique
de Tschirnhausen
(paramétrisation  ). |
 |
Voir aussi la développable
des tangentes à la parabole gauche.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2012