Les courbes  (G1) et (G2) sont parallèles si on peut déterminer des points courants respectifs M1 et M2 tels que  et . Pour une courbe de départ  de point courant , une parallèle est un ensemble (Ga) de points  où ,  l'angle  est l'angle de torsion (voir les notations). L'aire de la bande comprise entre deux arcs correspondants de (G0) et de (Ga) est égale à la longueur de l'arc médian de (Ga/2) fois a, ceci à condition que la bande ne se chevauche pas, et que a soit toujours inférieur au rayon de courbure.

Deux courbes sont dites parallèles si tout plan normal à l'une est un plan normal à l'autre ; on montre qu'alors la distance entre deux points de même plan normal est constante ; ne pas confondre avec des courbes translatées l'une de l'autre.

Deux courbes sont donc parallèles si ce sont les extrémités d'un segment de longueur constante se déplaçant toujours orthogonalement à sa direction, ce qui équivaut à ce que la droite portant ce segment possède une courbe enveloppe et roule sans glisser dessus ; cette courbe est alors la développée commune aux deux parallèles. Et les parallèles sont les développantes de cette courbe.

Plus concrètement, deux courbes parallèles peuvent donc être vues comme deux rails d'une voie ferrée reliés par des traverses de longueur constante, les traverses restant toujours orthogonales aux rails.

La relation de parallélisme des courbes 3D est une relation d'équivalence ; une classe d'équivalence
est l'ensemble des trajectoires des points liés à un plan qui roule sans glisser sur une surface développable, qui est la surface polaire commune à toutes ces courbes (d'où une correspondance bijective entre les surfaces développables et les classes d'équivalences de courbes parallèles).
Les courbes parallèles à une courbe sont donc les développantes de sa surface polaire.

La surface engendrée par les droites joignant deux points correspondant sur les deux parallèles est une surface développable (et toute surface développable est ainsi générée) : deux courbes sont donc paralèles si et seulement si ce sont deux trajectoires orthogonales des génératrices d'une surface développable.

Pour l'expression de la courbe parallèle, il faut bien prendre  et non  où  est le vecteur normal (le vecteur  est défini de façon à éliminer la torsion) :
 

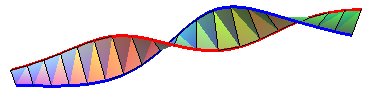
Un horoptère (en bleu) et une courbe du type Les "traverses" sont bien orthogonales à la courbe bleue, mais pas à la rouge.

Le même horoptère et une courbe parallèle, du type

Une courbe peut être parallèle à elle-même ; en plus des exemples dans le cas plan, il y a en 3D le bord d'un ruban de Möbius, dans le cas où sa représentation est développable, et le bord orthogonal aux génératrice de la surface.
 

Un ruban de moebius (à 3 demi-tours) à bord auto-parallèle (formé de bandes de 3 cônes centrés au sommets du grand triangle).

Les surfaces qui sont réunions de courbes parallèles deux à deux sont les surfaces de Monge.
 
 

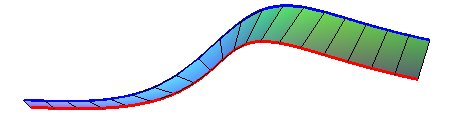
Les deux rails de ces voies de montagnes russes sont parallèles :

 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

Remerciements à Samuel Boureau pour son article "serpentins et tubes" dans le bulletin de l'APMEP, seul endroit où j'aie vu définir les parallèles dans l'espace.

© Robert FERRÉOL 2011