System of Cartesian equations: . Cartesian parametrization: . Rational 3D cubic.

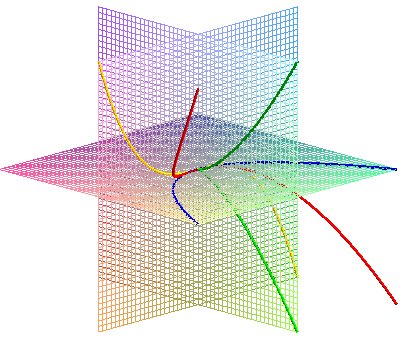
The skew (cubical) parabola is the curve with the above parametrization.
 

Its name comes from the fact that its projections on the planes xOy, xOz and yOz are a parabola, a cubical parabola, and a semicubical parabola.

 
 

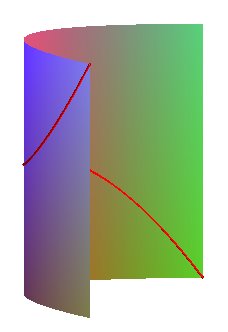
It is the intersection between three quadrics: (parabolic cylinder),  (hyperbolic paraboloid), and  (cone of revolution).

intersection of the cylinder and the paraboloid (that also share the line at infinity of the plane x = 0)

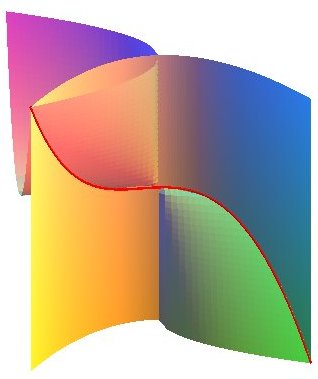
intersection of the cylinder and the cone (that also share the line Oz)

view of the 3 quadrics (Alain Esculier)

 

Its projection on the plane y + z = 0 is, up to scaling, a Tschirnhausen cubic (parametrization ).

See also the tangent developable of the skew parabola.
 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL 2018