Tangent developable

TANGENT DEVELOPABLE OF A CURVE

For an edge of parametrization :

, cartesian parametrization :

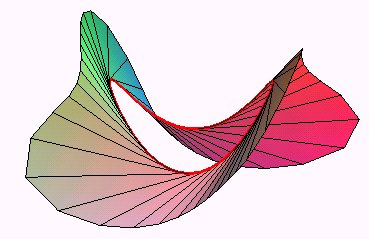
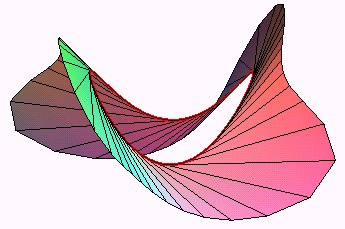
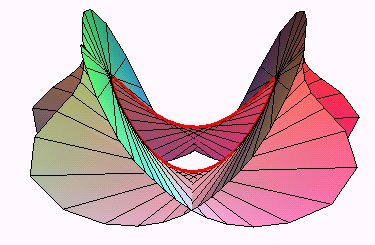
The tangent developable of a skew curve is the surface generated by the tangents to this curve; it is also the envelope of the osculating planes of the curve.

It is a developable surface the cuspidal edge of which is the curve .

Besides, any developable surface different from a cone or a cylinder is the tangent developable of the envelope of its generatrices.

EXAMPLES :

- the tangent developable of the circular helix is the developable helicoid.

- the tangent developable of the conical helix is named conical developable hélicoid although it is not a hélicoid.

The curve is algebraic iff its associated developable also is (?).
The algebraic developable surfaces (other than the cones and cylinders) of lowest degree are of degree 4, and they are the developables associated to the skew cubic curves.
Opposite, the tangent developable of the skew parabola , with Cartesian equation: .
Here are some other algebraic developables :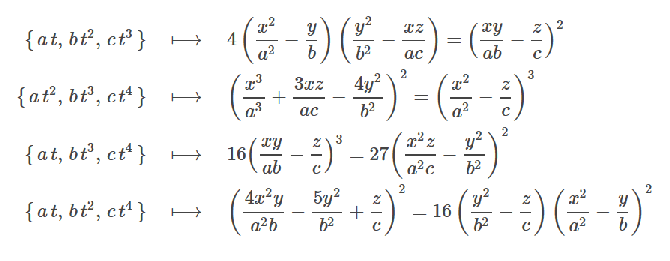
(Mo Li, China)

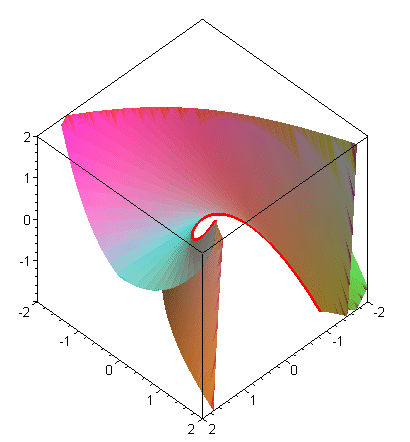Tangent developable by Patrice Jeener.

- the tangent developable of the conical helix is named conical developable hélicoid although it is not a hélicoid.
The curve is algebraic iff its associated developable also is (?). The algebraic developable surfaces (other than the cones and cylinders) of lowest degree are of degree 4, and they are the developables associated to the skew cubic curves. Opposite, the tangent developable of the skew parabola , with Cartesian equation: . Here are some other algebraic developables : (Mo Li, China)