Courbe étudiée par Terquem en 1845. [loria] p. 146

 

Paramétrisation cartésienne :  où  est le demi angle au sommet du cône et  , étant l’angle que fait l’hélice avec les génératrices. Équation cylindrique : . Équation sphérique :  ( est la colatitude). Pente constante de l'hélice par rapport au plan xOy : . Abscisse curviligne comptée à partir du sommet : . Rayon de courbure : . Rayon de torsion : .

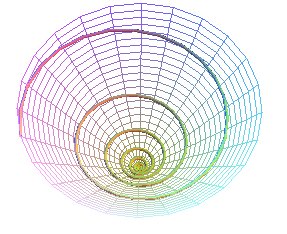
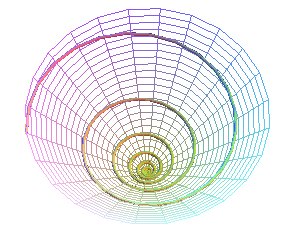
L'hélice conique peut être définie comme une hélice tracée sur un cône de révolution (i.e. une courbe faisant un angle constant avec l’axe du cône), ou une loxodromie de ce cône (c'est-à-dire courbe faisant un angle constant avec les méridiennes) ; ce n'est pas une géodésique du cône.
Concrètement, on obtient donc une hélice conique lorsque l'on trace un chemin de pente constante sur un cône placé verticalement.

La projection sur xOy est une spirale logarithmique () qui est aussi le lieu des sections des tangentes avec xOy ; la courbe obtenue par développement du cône en est aussi une spirale logarithmique.
Comme pour toute hélice, c'est une géodésique du cylindre vertical construit sur la spirale projection sur xOy.
La normale principale est constamment perpendiculaire à Oy.
Les rayons de courbure et de torsion sont proportionnels à z .
L’hélice est dextre lorsque  (elle “monte” dans le sens des aiguilles d’une montre) et senestre lorsque  (elle “monte” dans le sens trigonométrique).

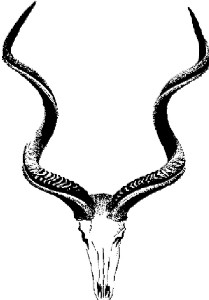
Un peu de biologie : la plupart des coquillages s’enroulent suivant des hélices coniques dextres, mais de très rares espèces s’enroulent suivant des hélices senestres (on reconnaît un coquillage dextre à ce que son ouverture se trouve à droite, lorsqu’elle est placée face à l’observateur, la pointe en haut) ; chez les animaux à corne tressée, la corne de droite est senestre, celle de gauche est dextre (et la licorne ?).
 

Voir aussi la spirale d'Ekman en géographie.

Ne pas confondre l'hélice conique avec la spirale conique de Pappus, dont les spires sont équidistantes :  l'hélice conique est à la spirale logarithmique ce que la spirale conique de Pappus est à la spirale d'Archimède. Et le sommet du cône est un point asymptote de l'hélice conique, qui n'est tracée que sur un demi-cône, tandis que c'est un simple point de passage de la spirale conique, tracée sur le cône complet.
Il ne faut pas non plus la confondre avec la spirale conique hyperbolique...

Par contre, l'hélice conique est un cas particulier de spirale conique de Pirondini.
 

les 4 dragons entrelacés de la bourse de Copenhague

 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2013