Équation sphérique : . Équation cylindrique : . Paramétrisation cartésienne : .

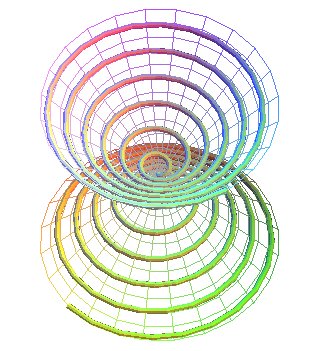
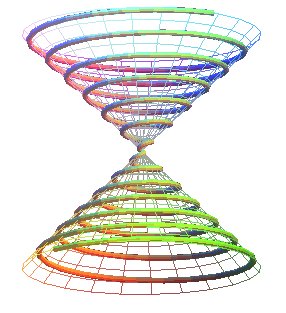
La spirale conique de Pappus est la trajectoire d'un point se déplaçant uniformément sur une droite passant par un point O, cette droite tournant uniformément autour d'un axe Oz en conservant un angle a avec Oz.
Elle est donc intersection du cône de révolution  (C) :  avec l’hélicoïde droit : .
Si l’on développe le cône (C) sur un plan, le point M devenant le point de coordonnées polaires , la spirale de Pappus devient la spirale d’Archimède : , autrement dit, la spirale de Pappus est un enroulement conique de spirale d’Archimède.

La projection sur xOy est aussi une spirale d’Archimède, qui coïncide avec la spirale de Pappus pour  : la spirale conique de Pappus est un relèvement conique de spirale d'Archimède.

La spirale de Pappus est la podaire de l'hélice circulaire par rapport à un point de son axe, c'est à dire le lieu des projetés de ce point sur les plans osculateurs à l'hélice.

La trace sur xOy de sa tangente est la spirale de Galilée : .
La trace sur xOy de la droite orthogonale à la courbe et incluse dans le plan tangent au cône est le cercle de centre O et de rayon .

Il ne faut pas la confondre avec l'hélice conique : la spirale conique de Pappus est à la spirale d'Archimède, ce que l'hélice conique est à la spirale logarithmique ! Ne pas confondre non plus avec la spirale conique de Pirondini.

Les projections planes des spirales coniques de Pappus sont les spirales Doppler.

Voir aussi les surfaces hélico-coniques, qui sont réunions de spirales coniques.
 

Gravure de wentzel Jamnitzer Perspectiva corporum regularium

Au Vietnam, spirales d'encens utilisées pour faire des voeux rédigés sur le carton jaune qui pend au milieu.

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2014