Équation cartésienne :

La spirale Doppler est la projection dans un plan fixe d'un mouvement en spirale d'Archimède uniforme situé dans un plan en translation uniforme. L'appellation "spirale Doppler" vient de l'analogie avec l'effet Doppler concernant une onde dont l'émetteur est en mouvement.
Si le plan mobile est fixe (k = 0), la spirale n'est autre qu'une spirale d'Archimède.
 
 

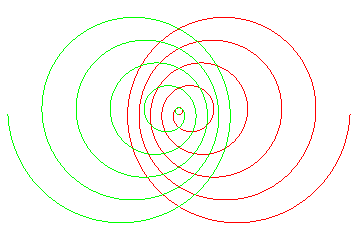
Cas 0 < k < 1

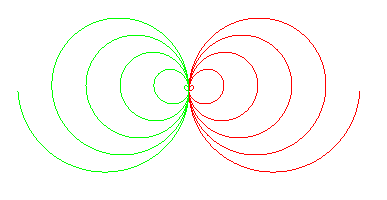
Cas k = 1

Cas k > 2

 
 

Les spirales Doppler sont les projections planes des spirales coniques de Pappus.

 
 

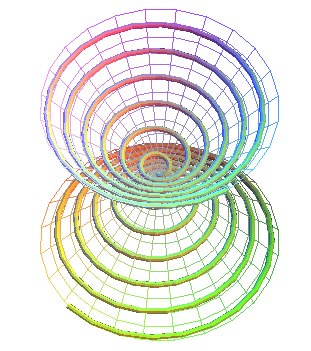courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2014