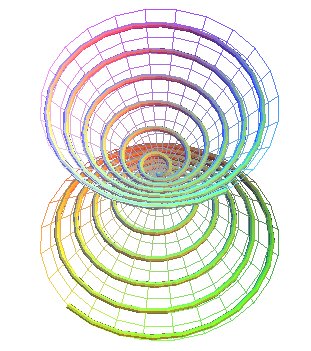
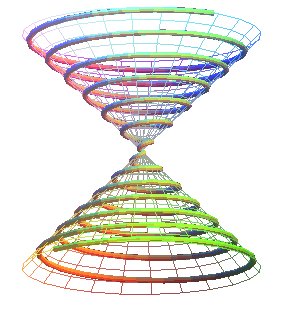
CONICAL SPIRAL OF PAPPUS
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
CONICAL SPIRAL OF PAPPUS


| Curve studied by Pappus, Pascal in 1779, and Chasles
in 1843.
Pappus: mathematician from Alexandria (4th century BC). |
| Spherical equation: Cylindrical equation: Cartesian parametrization: |
The conical spiral of Pappus is the trajectory of a point
that moves uniformly along a line passing by a point O, this line
turning uniformly around an axis Oz while maintaining an angle a
with respect to Oz.
Therefore, it is the intersection between the cone
of revolution (C):
and the right
helicoid:
.
If we develop the cone (C) on a plane, the point
M becoming the point with polar coordinates ,
then the Pappus spiral becomes the Archimedean
spiral:
,
in other words, the Pappus spiral is a conical coiling of an Archimedean
spiral.
The projection on xOy is also an Archimedean spiral,
which coincides with the Pappus spiral with :
the conical spiral of Pappus is a conical lift
of the Archimedean spiral.
The Pappus spiral is the pedal of the cylindrical helix with respect to a point on its axis, i.e. the locus of the projections of this point on the osculating planes of the helix.
The trace on xOy of its tangent is the Galilean
spiral: .
The trace on xOy of the line perpendicular to
the curve and included in the tangent plane of the cone is the circle with
center O and radius .
It must not be mistaken for the conical helix: the conical spiral of Pappus is to the Archimedean spiral what the conical helix is to the logarithmic spiral! Do not mistake it either for the conical spiral of Pirondini.
The planar projections of the conical spirals of Pappus are the Doppler spirals.
See also the helico-conical
surfaces, that are the reunions of conical spirals.
Engraving by wentzel Jamnitzer Perspectiva corporum regularium |
 |

In Vietnam, spirals of incense used to make wishes written on the yellow cardboard that hangs in the middle come true. |
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2018