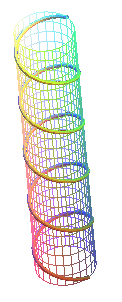
left-handed helix
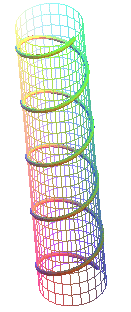
right-handed helix
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
CYLINDRICAL HELIX
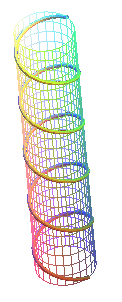
left-handed helix |
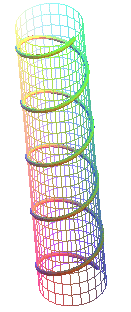
right-handed helix |
| First study (that did not reach our times) credited to
Apollonius of Perga (2nd century BC) and second study by Geminus of Rhodes
(1st century BC).
Other name: circular helix. |
Cartesian parametrization: 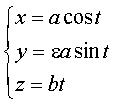 System of cylindrical equations: Curvilinear abscissa: Radius of curvature: Radius of torsion: Length of a coil: Center of curvature: |
The cylindrical helix can be defined as a helix
traced on a vertical cylinder
of revolution, or a rhumb
line of this cylinder (i.e., in both cases, a curve forming a constant
angle with respect to the axis of the cylinder), or a geodesic
of this cylinder (in other words, a curve that becomes a line when the
cylinder is developed) or a solenoid
with linear bore.
Intrinsic characterization: constant curvature and torsion.
The radius of the helix is a, and its shift
is (it
is the distance between two consecutive coils) and b is sometimes
called reduced shift of the helix. The angle of the helix
is the constant angle (equal to
)
formed by its tangent with respect to any plane orthogonal to Oz.
The helix is right-handed when e
= 1 (it “goes up” counterclockwise and an observer located outside of it
sees it going up from left to right) and left-handed
when e = - 1 (it “goes up” clockwise).
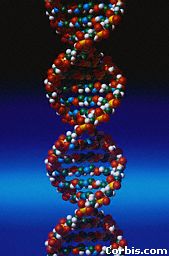
The DNA spirals along a double right-handed helix. |

 |
 |
Finally, in Brazil, a species of bat flying invariably along right-handed helices has been observed.
The trajectories of a charge placed in a uniform magnetic
field and subject to the Laplace force is a cylindrical
helix with axis parallel to that of the field (or a circle if the velocity
is perpendicular to the field, a straight line if it is parallel). Same
result for an inelastic flexible wire carrying a continuous electric current
placed in the field (and not subject to gravity). The shape assumed by
this wire was called by Riebke "electrodynamic catenary", and is in fact
a cylindrical helix, with the same limit case as before.
| Proof of this fact:
Newton's second law and the expression of the Laplace force give: The first Frenet formula The radius of torsion of the helix, classically given by |
Nota: why are the blade-based propelling systems for boats or planes called helices? It is because when the boat moves with constant speed, the motion of the helix with respect to a fixed frame is a helicoidal motion, and all its points describe cylindrical helices.
For the projections of the cylindrical helix, see at trochoid,
cochleoid
and
hyperbolic
spiral.
See also the helicoids,
the other cylindrical curves,
the coil (tube
with a cylindrical-helix-shaped bore), and the revolution
of the sinusoid.
More beautiful images by Amain Juhel.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL, Jacques MANDONNET 2018