Conical helix

CONICAL HELIX

Curve studied by Terquem in 1845.
Other name: concho-spiral.
[loria] p. 146

Cartesian parametrization: where is the half-angle at the vertex of the cone and , with the angle between the helix and the generatrices.
Cylindrical equations: .
Spherical equation: .
Constant slope of the helix with respect to the plane xOy: .
Curvilinear abscissa based on the vertex: .
Radius of curvature: .
Radius of torsion: .

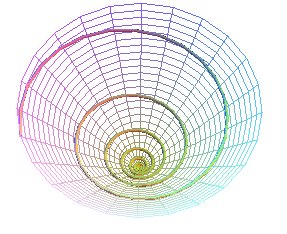
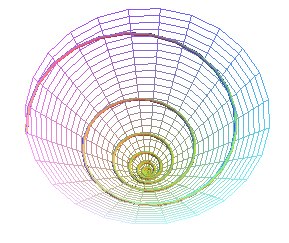
The conical helix can be defined as a helix traced on a cone of revolution (i.e. a curve forming a constant angle with respect to the axis of the cone), or a rhumb line of this cone (i.e. a curve forming a constant angle with the meridians); it is not a geodesic of the cone.
In concrete terms, we get a conical helix when we trace a path with constant slope on a cone placed vertically.

The projection on xOy is a logarithmic spiral (), which is also the locus of the intersection between the tangents and xOy; the curve obtained by developing the cone is also a logarithmic spiral.
As for all helices, it is a geodesic of the vertical cylinder based on the aforementioned spiral, projection of the curve on xOy.
The principal normal is always perpendicular to Oy.
The radii of curvature and torsion are proportional to z.
The helix is right-handed when (it “goes up” clockwise) and left-handed when (it “goes up” counterclockwise).

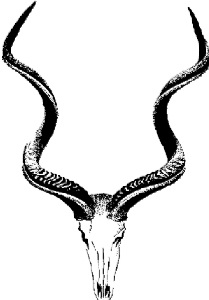
A little biology: most sea shells are wound along right-handed conical helices, but some very rare species are wound along left-handed spirals (a right-handed sea shell can be identified by the fact that its opening is on the right, when the shell is in front of the observer, its tip at the top); among animals with braided horn, the horn on the right is left-handed while that on the left is right-handed (what about the unicorn?).