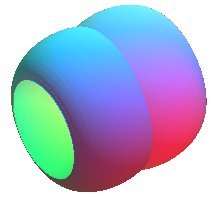
Surface studied by Delaunay in 1841, Lindelöf in 1863, Plateau in 1873.

 

Cartesian parametrization:  where  is the parametrization of the associated Delaunay roulette.

The Delaunay surfaces are the surfaces of revolution generated by the rotation of the Delaunay roulettes around their base.

The surfaces associated to an elliptic roulette are called onduloids and those associated to a hyperbolic roulette nodoids.
Since the parabolic roulette is the catenary, the associated surface is none other than the catenoid (case of the zero mean curvature).

The Delaunay surfaces have the remarkable property of being the only surfaces of revolution with constant mean curvature (if we include the sphere, which is a limit case), the case of zero curvature being obtained for the catenoid.

As a consequence, a layer of soap with an axis of revolution assumes the shape of a Delaunay surface.

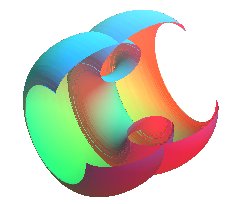
See also: Histoires de bulles et de doubles bulles, La Recherche, N°303 - 11/1997
and www.gang.umass.edu/gallery/cmc/
 

next surface

previous surface

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL , Jacques MANDONNET 2017