Radioïde

RADIOÏDE
Radioid

Courbes étudiées par Wilhelm Nördling en 1867, L. Fargue en 1868, Emile Turrière en 1939.
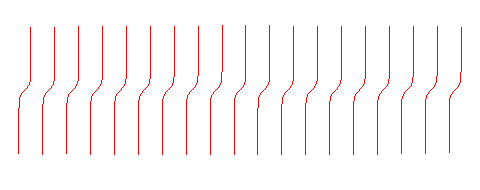
Voir cet article sur les voies ferrées, dont la figure ci-dessus est tirée.

Les radioïdes sont les courbes permettant de raccorder un segment de droite à un arc de cercle, de sorte que la courbure varie continûment, ceci en vue d'applications ferroviaires ou routières : un passager d'un véhicule roulant le long de cette courbe subira une force centrifuge variant elle aussi continûment, ce qui n'est pas le cas pour une courbe formée d'un segment de droite et d'un arc de cercle.

Toute courbe de classe C² ayant un point de courbure nulle peut être considérée comme une radioïde, mais ont été utilisées en pratique :

    - la courbe élastique (dite radioïde aux abscisses : courbure proportionnelle à l'abscisse)
    - la parabole cubique ou parabole de Nördling : y = x³ qui approxime la précédente au niveau du point d'inflexion
    - la clothoïde (dite radioïde aux arcs : courbure proportionnelle à l'abscisse curviligne)
    - la spirale de Norwich (dite radioïde aux cordes : courbure proportionnelle à la distance à un point fixe)
    - la radioïde pseudo-elliptique, étudiée ci-dessous

RADIOÏDE PSEUDO ELLIPTIQUE
Pseudo elliptical radioid

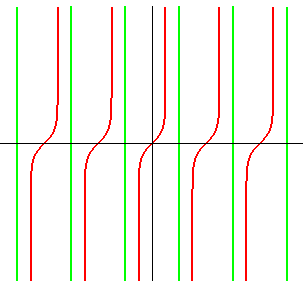Équation cartésienne :

qui pour

se met sous les formes équivalentes :
y = a gd^-1 (x/a) = ln (tan(x/2a + p/4)) = argsh(tan x/a) = argth(sin x/a) = signe(x).argch(sec(x/a)) , où gd^-1 est la fonction de Gudermann inverse.
Courbe transcendante.
Paramétrisation cartésienne :

.
Angle tangentiel cartésien :

.
Abscisse curviligne :

(intégrale pseudo-elliptique, d'où le nom de la courbe), où

.
Courbure :

La radioïde pseudo-elliptique est la courbe de la fonction de Gudermann inverse. Elle ressemble à la tangentoïde, mais son intéret vient de ce que l'abscisse curviligne se calcule à l'aide des fonctions usuelles, et non à l'aide de fonctions elliptiques comme pour la tangentoïde.
C'est la courbe d'une loxodromie de la sphère en coordonnées géographiques.

courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres