Paraboloïde de révolution

PARABOLOÏDE DE RÉVOLUTION
Paraboloid of revolution, Drehparaboloid

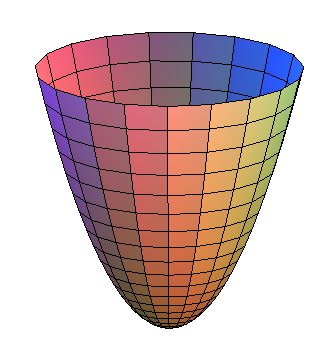
Le paraboloïde de révolution est la surface obtenue en faisant tourner une parabole autour de son axe.

Équation cylindrique : .
Équation cartésienne : .
Quadrique.
Paramétrisation cartésiennes :

où les lignes de coordonnées sont les cercles parallèles et les paraboles méridiennes :
(). où les lignes de coordonnées sont des paraboles parallèles à l'axe :
autres paraboles :
ellipses :

Première forme quadratique fondamentale : .
Élément d'aire : .
Deuxième forme quadratique fondamentale :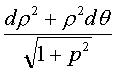
Courbure totale :
Tous les points sont elliptiques et il y a un ombilic : le sommet O.

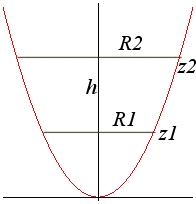
Volume du bol paraboloïdique de hauteur h, le cercle sommital étant de rayon R () : (moitié du cylindre circonscrit).
Aire de ce bol : ; approximation pour h petit : .

Volume du tronc de paraboloïde limité par les plans d'équation z = z₁ et z = z₂ : (comparer avec le tronc de cône, et le tronc de neiloïde).

Le paraboloïde de révolution est aussi la surface de translation obtenue en translatant une parabole le long d'une parabole égale tournée de 90°.

Courbes remarquables tracées sur le paraboloïde de révolution :
- les lignes de courbure, qui sont les parallèles (cercles) et les méridiennes (paraboles).
- il n'y a pas de ligne asymptotique.

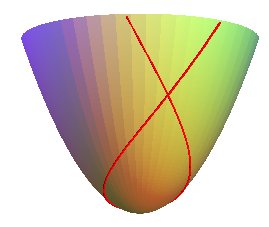
Les géodésiques sont les courbes solutions de : .
Ce sont des relèvements d'hypercycloïdes :
Paramétrisation (avec )

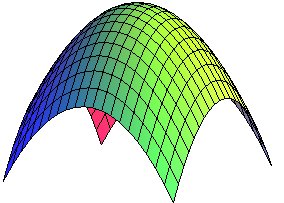
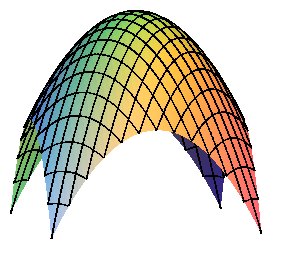
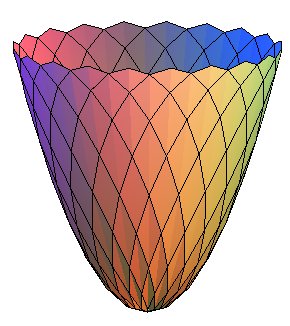
- les hélices.

- les vasques 3D.

On obtient physiquement un paraboloïde de révolution en faisant tourner un liquide à vitesse constante autour d'un axe.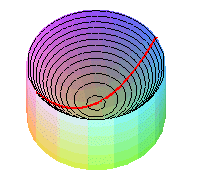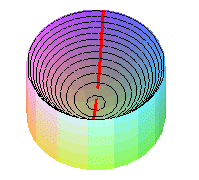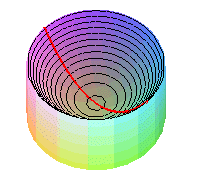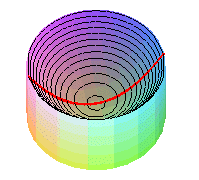

Voir plus généralement les paraboïdes elliptiques.

On peut aussi faire tourner la parabole autour d'une droite perpendiculaire à son axe.
On obtient une surface, appelée paraboloïde de Flamm par les astrophysiciens, ressemblant à un hyperboloïde de révolution, mais de degré 4.
Équation cylindrique : , équation cartésienne : .
Paramétrisation cartésienne : .
Aire pour : .
Pour b = a/2, l'axe de rotation est la directrice des paraboles, et on obtient une surface dont les courbures parallèle et méridiennes sont dans le rapport – 2.

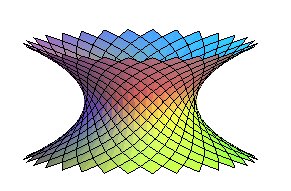En dendométrie, pour calculer le volume d'un tronc dont la surface est à courbure positive, on utilise la formule du tronc de paraboloïde vue ci-dessus, comme indiqué sur la figure ci-contre :

Le four solaire d'Odeillo dans les Pyrénées.
Voir le principe à parabole.
Antenne parabolique

surface suivante surface précédente courbes 2D courbes 3D surfaces fractals polyèdres

où les lignes de coordonnées sont les cercles parallèles et les paraboles méridiennes : ().	où les lignes de coordonnées sont des paraboles parallèles à l'axe :	autres paraboles :	ellipses :

Première forme quadratique fondamentale : . Élément d'aire : . Deuxième forme quadratique fondamentale : Courbure totale : Tous les points sont elliptiques et il y a un ombilic : le sommet O.
Volume du bol paraboloïdique de hauteur h, le cercle sommital étant de rayon R () : (moitié du cylindre circonscrit). Aire de ce bol : ; approximation pour h petit : .
Volume du tronc de paraboloïde limité par les plans d'équation z = z₁ et z = z₂ : (comparer avec le tronc de cône, et le tronc de neiloïde).