k > 1	0 < k < 1	-1 < k < 0	k < -1

 

Surface étudiée par Hopf en 1951, et Wolfgang Kühnel en 1999 (Differential Geometry, p. 95)

 

Paramétrisation cylindrique : 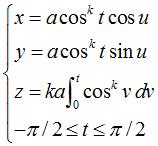, paramétrisation cartésienne : . Équation différentielle :  ou  où . Rayons de courbure parallèle et méridien : .

Il s'agit de la surface de révolution dont les deux rayons de courbure principaux (ou bien les deux courbures principales, ou encore la courbure moyenne et la courbure totale) sont proportionnel(le)s en tous points  - voir les notations. Il s'agit donc d'une surface de Weingarten.

Le rayon de courbure méridien d'une surface de révolution étant celui du profil de cette surface, et le rayon de courbure parallèle étant la longueur du segment MN joignant le point M de la surface au point N d'intersection de la normale avec l'axe, les profils des surfaces étudiés ici ne sont autres que les courbes dont le rayon de courbure est proportionnel à la normale (ou ce qui est équivalent telles que le quotient MI / MN est constant - égal ici à k -, I étant le centre de courbure), autrement dit, les courbes de Ribaucour.
 

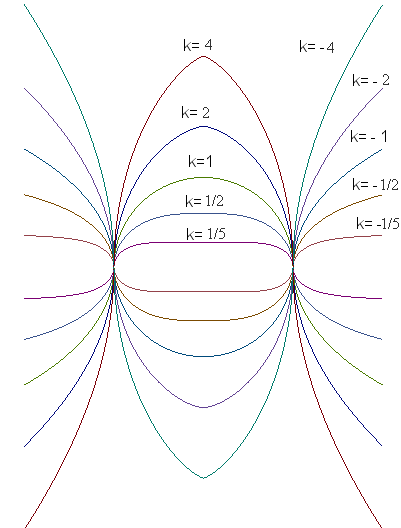
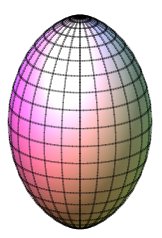
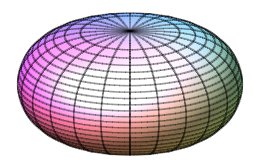
Diverses coupes par un plan passant par l'axe ;  pour k = 1 on obtient le cercle, pour k = 2 la cycloïde, pour k = 1/2 la lintéaire droite, pour k = –1 la chaînette, et pour k = – 2 la parabole (de directrice Oz).	Vue des demi-surfaces pour k = 2, k = 1 (sphère), k = 1/2, et k  = 1/5.  Notons que la relation  ne vaut pas pour le point d'intersection avec l'axe, qui est singulier pour k > 1/2 et un ombilic pour .	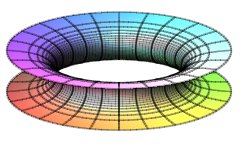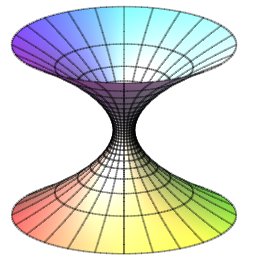Vue des demi-surfaces pour k = – 2 (paraboloïde de Flamm) et k = –1 (caténoïde).

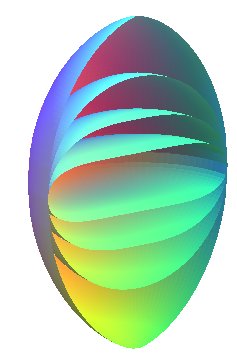Comparer avec les surfaces de révolution à courbure de Gauss constante (autrement dit, dont les deux courbures sont inversement proportionnelles).
 

surface suivante

surface précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2019