Pour une surface de départ (S0)  de point courant , une parallèle est un ensemble (Sa) des points .

Deux surfaces sont dites parallèles si toute normale à l'une est une normale à l'autre ; on montre qu'alors la distance entre deux points à normale commune est une constante, appelée distance de parallélisme ; ne pas confondre avec des surfaces translatées l'une de l'autre.

Comme pour les plans, la relation de parallélisme des surfaces est une relation d'équivalence.

Les surfaces parallèles à une surface (S₀) sont les surfaces (S_a), parallèle d'indice a à (S₀), obtenues en reportant algébriquement une "longueur" a à partir des points de (S₀) sur la normale orientée, autrement dit le lieu des points M =    où  est le vecteur normal en M₀. La relation de parallélisme étant symétrique, (S₀) est aussi parallèle à (S_a).

La réunion de (S_a) et (S_-a) est l'enveloppe des sphères de rayon a centrées sur (S₀).

Les points singuliers des surfaces parallèles décrivent la focale de la surface de base ????
 

Une notion voisine est la notion de surface de niveau de la fonction "distance (d'un point de l'espace) à la surface". Ces surfaces de niveaux sont formées de portions de surfaces parallèles et de portions de sphères, et présentent l'intérêt de constituer une partition de l'espace, contrairement aux surfaces parallèles.
 
 

Ci-contre, animation obtenue par la succession de diverses surfaces parallèles à un ruban de Moebius. La surface parallèle d'indice a est identique à celle d'indice -a, contrairement aux surfaces parallèles à un ruban normal.... De plus, cette surface possède la particularité d'être strictement parallèle à elle-même.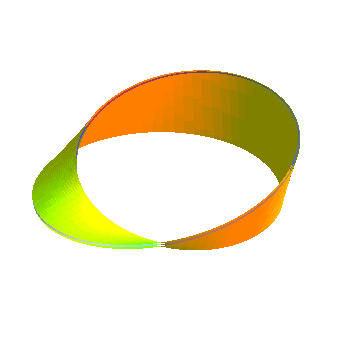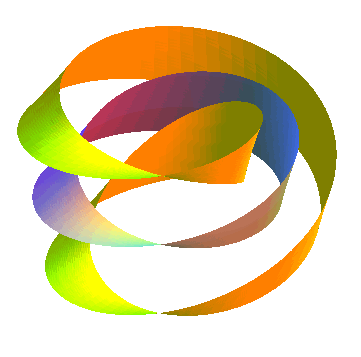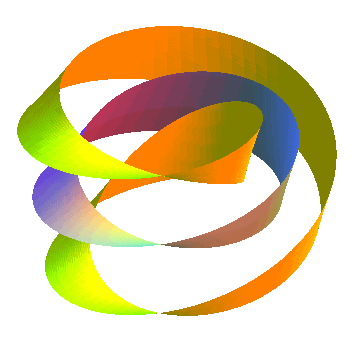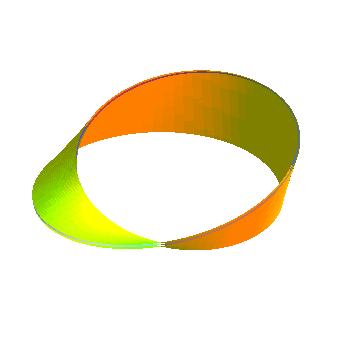

 
 

surface suivante

surface précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2012