Steven Anson Coons (1912-1979) : informaticien américain.

 

Etant donnés quatre arcs paramétrés sur [0,1]  tels que  Le patch de Coons est la surface paramétrée par  où ,  et  de sorte que .

Le patch de Coons fournit une méthode pour construire une surface s'appuyant sur un contour donné, lorsque celui-ci est formé de 4 arcs de courbes.

Exemples :

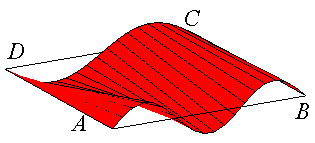
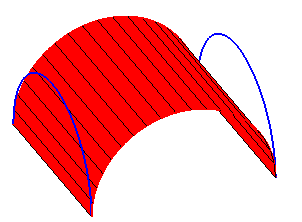
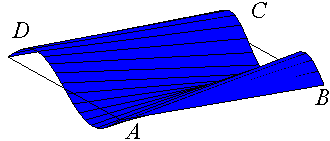
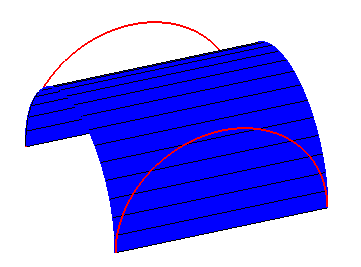
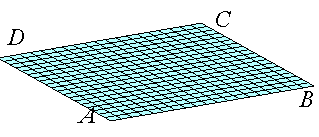
Première surface réglée paramétrée par M1  joignant les points P1(t) aux points Q1(t).	Deuxième surface réglée paramétrée par M2 joignant les points P2(u) aux points Q2(u).	Patch bilinéaire paramétré par M3  portion de paraboloïde hyperbolique s'appuyant sur le quadrilatère gauche ABCD. Le patch est plan si les 4 sommets sont coplanaires.	Patch de Coons final M1 + M2 - M3
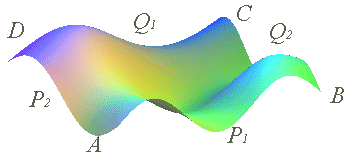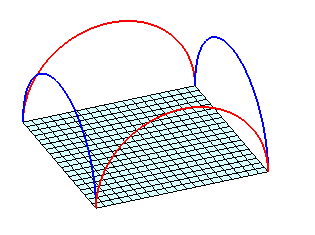
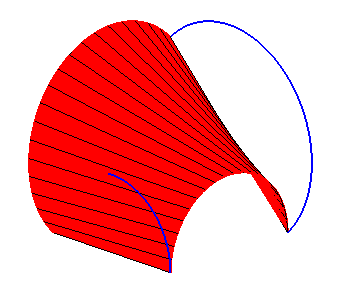
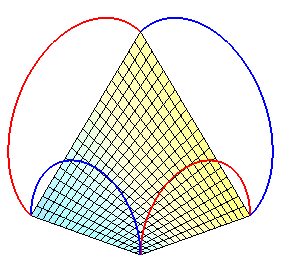
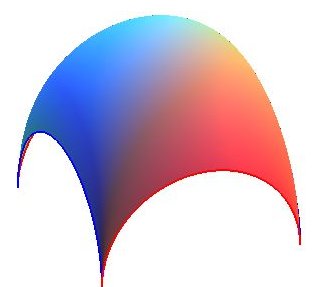
		Bord formé de 4 arcs de cercles de même rayon	On obtient un dôme de Bohème

 
 

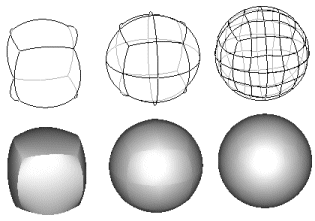
Réalisation d'une sphère par patchs de Coons

Oeuf réalisé par assemblage de patchs de Coons réalisé par Alexandre Demir, pour le prix du meilleur ouvrier de France.

Voir aussi les surfaces de Bézier.
 

surface suivante

surface précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2023