
Un B(1,1,1)

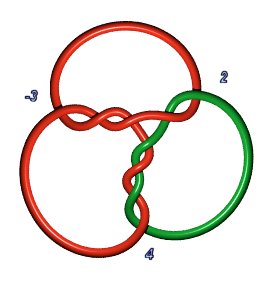
Un B(3,-2,-2,2) réalisé par Sandjer, pâtissier à bretzel love.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
NOEUD, ENTRELACS DE BRETZEL
Pretzel
knot, link, Brezelknoten, Brezelverschlingung

Un B(1,1,1) |

Un B(3,-2,-2,2) réalisé par Sandjer, pâtissier à bretzel love. |
| Wikipedia anglais |
| Appelant "enlacement d'ordre p" un enlacement
à |p| croisements de deux hélices circulaires, tournant
dans le sens, trigonométrique si p est > 0, contraire sinon,
l'entrelacs de bretzel |
 |
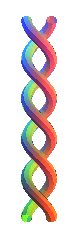 Enlacement d'ordre -5 |
 formé de deux brins. |
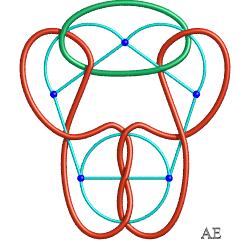
| On peut aussi caractériser les entrelacs de bretzel
par le fait que leur graphe
associé possède n sommets placés en cercles
avec une succession d'arêtes multiples d'ordres Par exemple, le graphe bleu ci-contre est associé à B(3,2,2). |
 |
Le nombre de brins est égal au nombre de
qui sont pairs, s'il y en a au moins un de pair. Si tous les
sont impairs, il y a un ou deux brins suivant que n est impair ou
pair.
Si tous les
sont positifs, l'entrelacs est alterné avec
croisements.
Les 6 premiers noeuds premiers peuvent être vus
comme des noeuds de bretzel à coefficients > 0 :
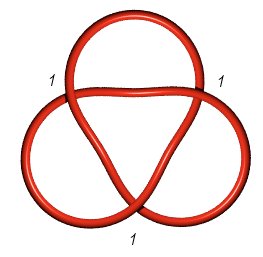
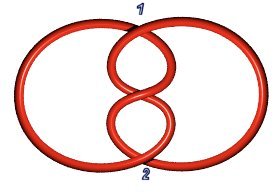
| Noeud de trèfle
3.1.1 : |
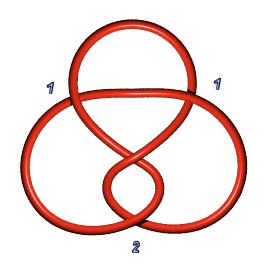
Noeud de huit
4.1.1 : |
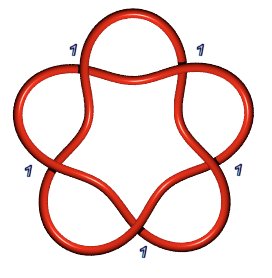
Noeud 5.1.1
: |
  |
 |
  |
|
|
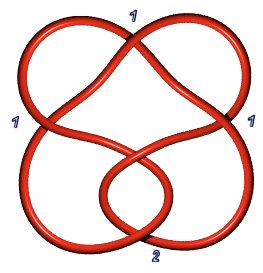
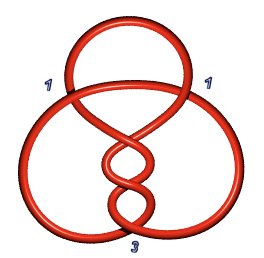
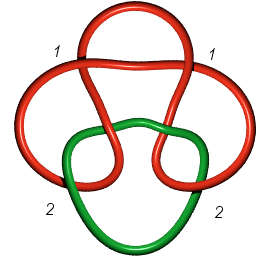
Noeud d'arrimeur
6.1.1 : |
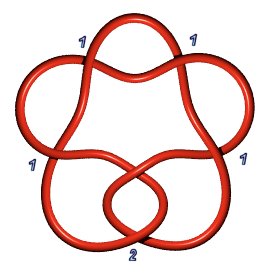
Noeud 6.1.2
: |
 |
 |
 |
Ce n'est par contre pas le cas du suivant (6.1.3) : .
Pour n impair, le noeud de bretzel
avec n "1" est équivalent au noeud
torique T(n,2).
Les six premiers entrelacs premiers sont eux aussi obtenables
comme entrelacs de bretzel à coefficients > 0:
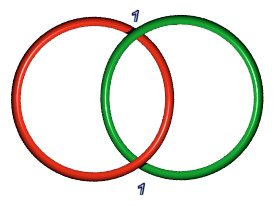
| Entrelacs de Hopf 2.2.1 : B(1,1) | Noeud de Salomon 4.2.1: B(1,1,1,1) ou B(2,2) ou B(a,b), a+b = 4 | Entrelacs de Whitehead 5.2.1 : B(1,2,2) |
 |
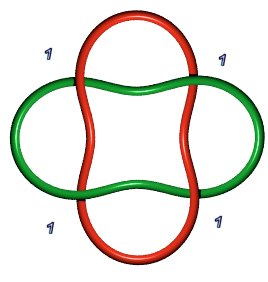
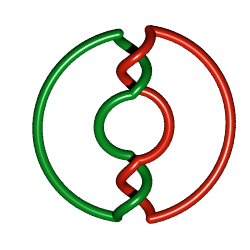 |
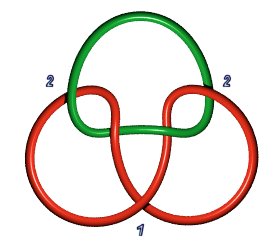 |
|
|
|
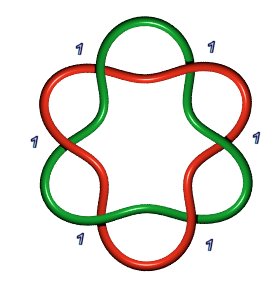
Sceau de Salomon 6.2.1 : B(1,1,1,1,1,1) ou B(a,b), a+b=6 |
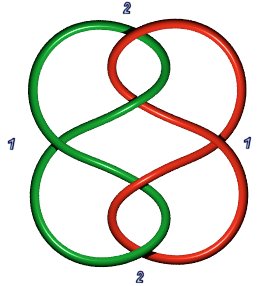
 |
 |
 |
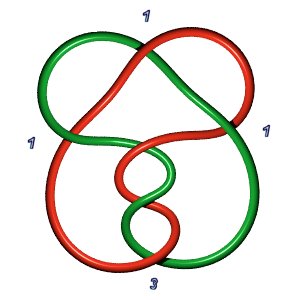
L'entrelacs 6.3.2
(anneaux de Borromée) n'est pas un bretzel, mais 6.3.1
est B(2,2,2) : 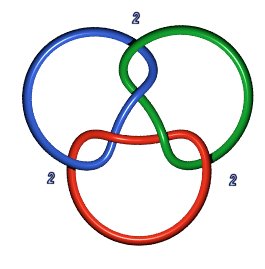
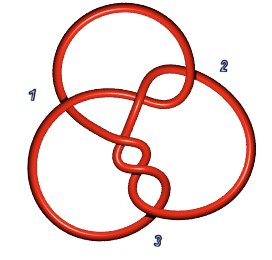
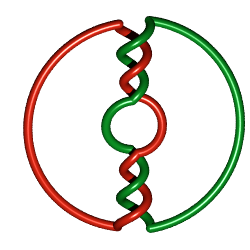
| Lorsque certains La troisième vue montre le noeud B(2,–3,–3) qui a huit croisements apparents et a bien huit pour nombre minimal de croisements, voir la page du 8.1.19. |
 |
.png) |
 |

Un vrai bretzel alsacien !
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL
2016