Lorsque n points M₁, M₂,…, M_n (traditionnellement, des chiens, des souris, des fourmis, des punaises, des coccinelles, ou des mouches, ...) se poursuivent mutuellement, chacun à vitesse constante, M_k poursuivant M_k+1 (et M_n poursuivant M₁), les trajectoires de ces points sont des courbes de poursuites mutuelles.
Les mouvements et les trajectoires des poursuivants sont alors régis par le système différentiel formé par les n relations .
Il est à noter que lorsque  est proportionnel à  le système devient linéaire et se résout exactement.

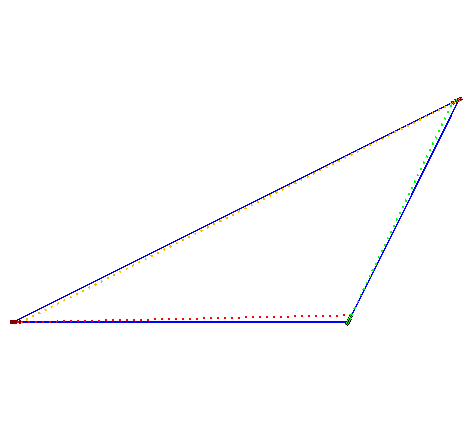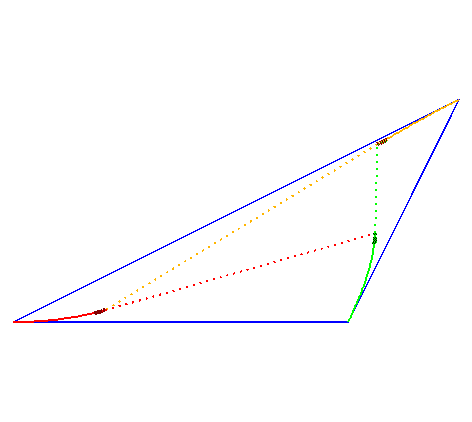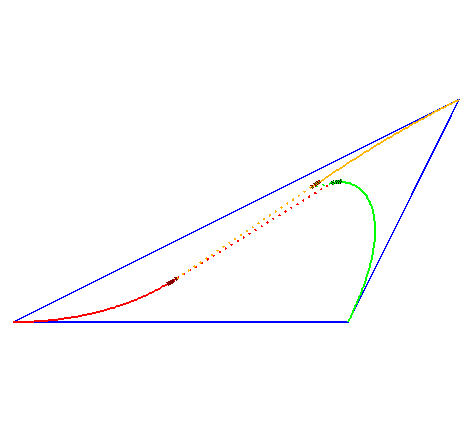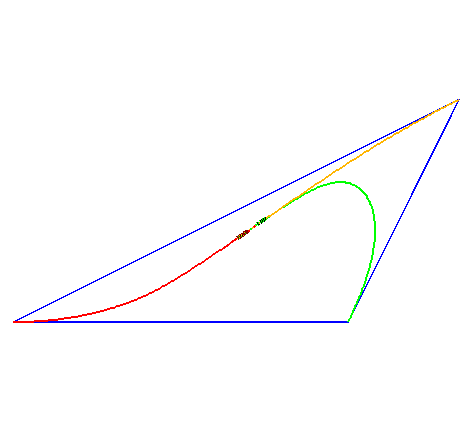
Cas d'un triangle ABC (A poursuivant B, poursuivant C, poursuivant A)

Cas où les chiens ont la même vitesse. On remarque dans le cas particulier ci-contre que les deux chiens qui étaient les plus éloignés au départ sont ceux qui se rencontrent en premier !
Cas de vitesses quelconques. R. K. Miller a déterminé en 1871 que le triangle reste semblable à lui-même si et seulement si les vitesses respectives de A,B,C sont proportionnelles à  (notations classiques des côtés d'un triangle). Dans ce cas, le premier point de Brocard du triangle formé par les chiens reste fixe et les chiens se rencontrent simultanément en ce point ; de plus, les courbes décrites sont des spirales logarithmiques, en conséquence de la définition tangentielle de ces dernières.
Si chaque chien a une vitesse proportionnelle à la distance au chien suivant, soit , le point de coordonnées barycentriques  dans (A, B, C) reste fixe et les chiens se rencontrent simultanément en ce point. Les chiens peuvent donc converger en n'importe quel point à l'intérieur du triangle. Ceci se généralise à un polygone convexe (à droite)

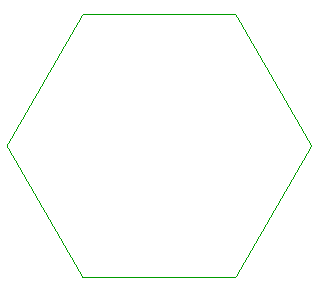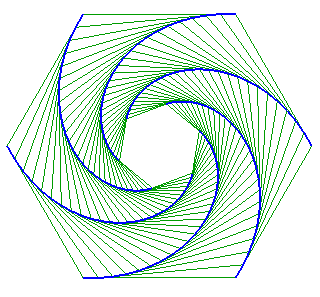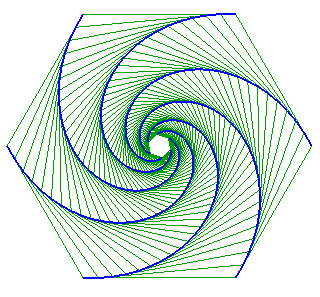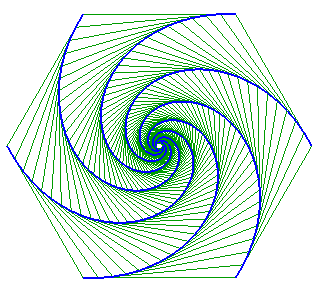
Lorsque la figure de départ est un polygone régulier convexe, chaque point poursuivant le sommet suivant (un sens de parcours sur le polygone étant choisi), et les vitesses sont égales, les trajectoires sont des spirales logarithmiques de point asymptote le centre du polygone.
Le paramètre de la spirale est , l'angle tangentiel polaire constant étant donc de où n est le nombre de côtés du polygone.
La longueur de la trajectoire de chaque chien est donc égale à  où R est le rayon du polygone, , la longueur du côté.
Par exemple : .
 

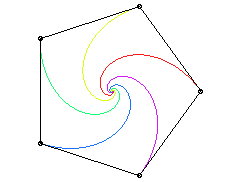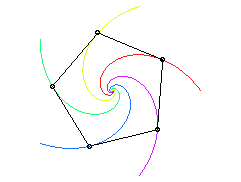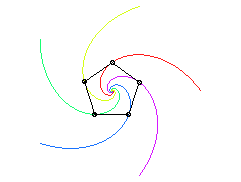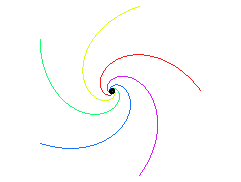
Cas d'un pentagone	Cas d'un hexagone Notons que les courbes sont des développantes obliques les unes des autres.	Cas d'un octogone

 

Démonstration dans le cas d'un carré. Les chiens forment constament un carré EFGH avec les coordonnées indiquées sur la figure. La colinéarité du vecteur vitesse en E avec  , se traduit par , d'où l'équation différentielle de la courbe :  . En passant en coordonnées polaires l'équation se transforme en , d'où la solution , avec a = 1 en appliquant la condition initiale. Une paramétrisation est donc  ; avec celle-ci, la vitesse des chiens est , elle décroit vers 0, et le temps de parcours est infini, pour une longueur  (côté du carré de départ ). Avec , les chiens ont une vitesse constante égale à , pour un temps de parcours égal à 1.

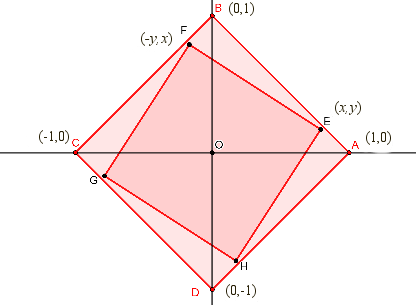
Figure : Elisabeth Busser

 

Cas d'un carré, reproduit 4 fois  par symétries

Cas d'un triangle équilatéral, reproduit 6 fois par symétries

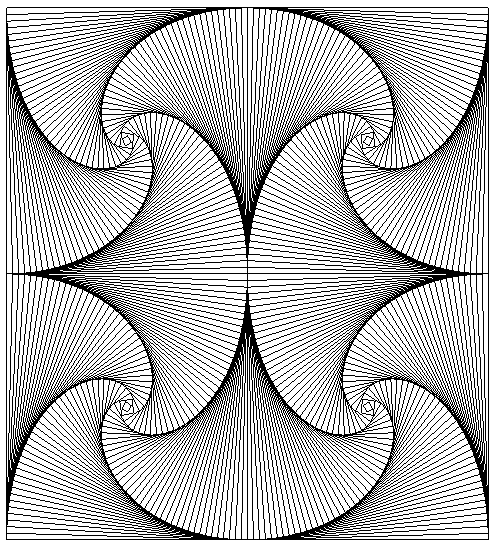Voir aussi de telles courbes en 3D.
 

L'artiste ivoirien anonyme créateur de cette gravure pensait-il tracer des courbes de poursuite ?

 
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL, Alain ESCULIER  2023