On appelle courbe de poursuite (en navigation) parallèle la trajectoire d'un point mobile M (le suiveur) suivant un autre point mobile M₀ (le fuyard) de sorte que la droite (M₀M) (la ligne de vue) reste parallèle à elle-même au cours du temps.
C'est un cas limite de courbe de filature, lorsque l'"arbre" est placé à l'infini.

Le problème possède une solution déterminée si l'on impose une condition sur la vitesse de M. On considérera ici le cas où les vitesses V et V₀ de M et M₀  sont proportionnelles (V= kV₀) : la courbe de poursuite obtenue ne dépend pas de la loi de vitesse du fuyard.

La notion est alors involutive, en ce sens que la courbe de fuite est une courbe de poursuite associée à la courbe de poursuite de départ, si on change k en 1/k.
 

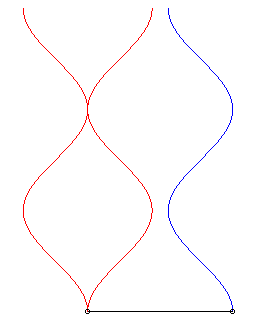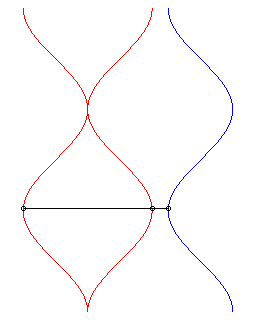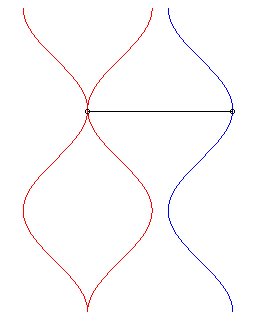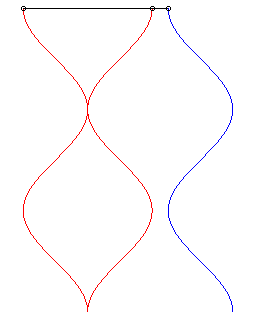
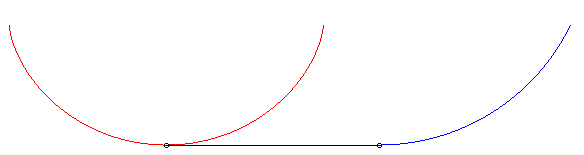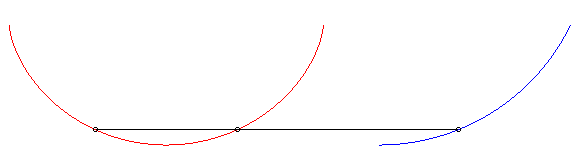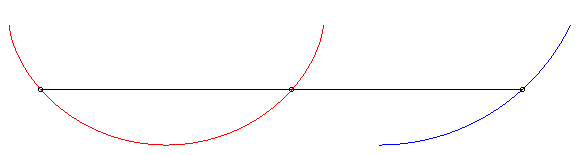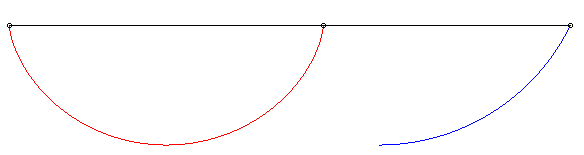
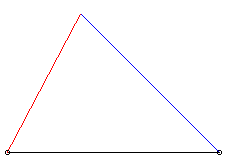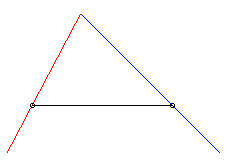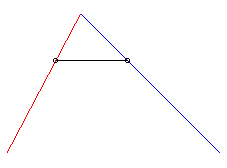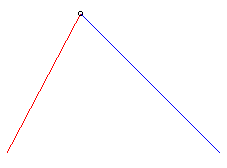
Pour k = 1 (suiveur et fuyard ont même vitesse) le mouvement du suiveur (2 possibilités en rouge ci-contre) est symétrique ou translaté de celui du fuyard.
Pour k > 1, il y a toujours 2 solutions symétriques pour le suiveur, l'une d'entre elle rattrapant toujours le fuyard (la seule que nous considérerons dorénavant).
Pour k <1, il n'y a pas toujours de solution, ou la solution peut n'exister que sur un certain laps de temps, cf. ci-contre.

 

Conditions régissant le mouvement du suiveur, en coordonnées cartésiennes : . Résolution dans un cas particulier recouvrant la généralité : au temps t = 0, le suiveur est en O et le fuyard sur l'axe Ox ; si la paramétrisation du mouvement du fuyard est , celle du suiveur est alors donné par :   (donc deux solutions symétriques par rapport à Oy).

Quelques cas particuliers :

     1) Le mouvement du fuyard est rectiligne.

La courbe de poursuite parallèle est alors, si elle existe, également rectiligne.
 

Mouvement du fuyard : , a > 0

Mouvement du suiveur :

Instant de la collision :

Lorsque k > 1 le suiveur rattrape bien toujours le fuyard ; exemple ci-contre avec  et k =1,5.
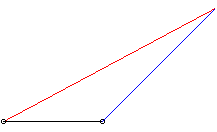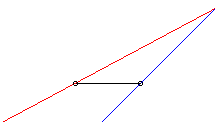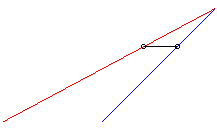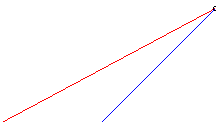Lorsque k1, il ne le rattrape que pour  et  ; exemple ci-contre avec  et k = 0,8.

REMARQUE : dans ce cas, la courbe de poursuite parallèle est en fait la courbe du chien intelligent, qui au lieu d'aller à tout instant dans la direction de son maître, va directement, vers le point où, compte tenu de sa vitesse et de celle du maître, il va le rencontrer en ligne droite. Dans le cas d'une trajectoire quelconque du fuyard, la navigation parallèle consiste donc à prendre à chaque instant la direction du chien intelligent, supposant que le fuyard va continuer en ligne droite. Ceci optimise le rattrapage du fuyard par le suiveur ; l'optimum serait bien sûr la courbe du chien devin, qui devinerait le mouvement de son maître et calculerait la direction à prendre pour une rencontre en ligne droite.

    2) Le mouvement du fuyard est circulaire.
 

Mouvement du fuyard :	Mouvement du suiveur :
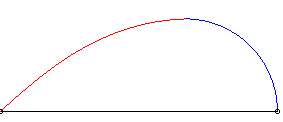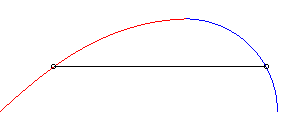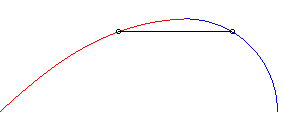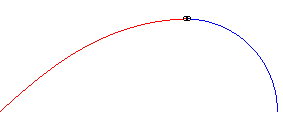
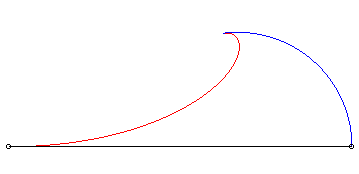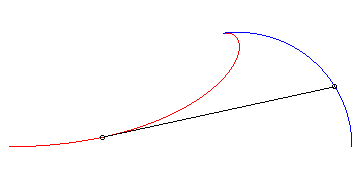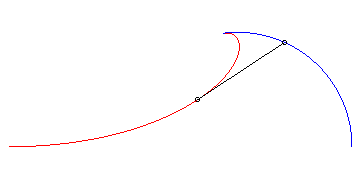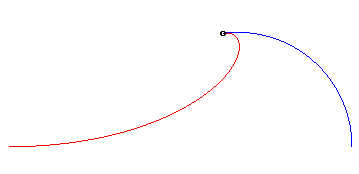
Exemple avec k = 1,5 et a = 2b	Comparaison avec la poursuite classique

La poursuite simple et la poursuite parallèle, sont des cas particuliers de la poursuite dite "en navigation proportionnelle" ; dans ce cas, la vitesse de rotation de la ligne de vue a une vitesse de rotation proportionnelle à celle du vecteur vitesse du suiveur. Si le rapport de proportionalité est k, le cas limite k = 0 correspond à la poursuite parallèle, et le cas k = 1 correspond à la poursuite simple (si le suiveur prend la direction du fuyard à l'instant initial).
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2011