Problème posé par Buray (alias Aubry) en 1896 (intermédiaire des mathématiciens p. 35 et 93) ; courbe étudiée par Turrière en 1915. Autres noms : courbe de poursuite en alignement, courbe de l'éclaireur, courbe du lion.

On appelle courbe de filature la trajectoire d'un point mobile M (le fileur) qui est à chaque instant aligné avec un point fixe O (l'arbre) et un autre point mobile M₀ (le filé). Ceci ne correspond bien sûr à une vraie filature que lorsque O se trouve entre M et M₀ , c'est-à-dire quand l'arbre cache M à la vue de M₀ .
Le problème possède une solution déterminée si l'on impose une condition sur la vitesse de M. On considérera ici le cas où les vitesses V et V₀ de M et M₀ sont proportionnelles (V= kV₀) :  la courbe de filature obtenue ne dépend pas de la loi de vitesse du filé.

La notion est alors involutive, en ce sens que la courbe du filé est une courbe de filature associée à la courbe de filature de départ, si on change k en 1/k.
 

Conditions régissant le mouvement du fileur, en coordonnées cartésiennes : . Équation différentielle des courbes de filature :  ( étant l'angle polaire relatif à O). D'où en coordonnées polaires : . Solution particulière évidente :  (la courbe de filature est homothétique de celle du filé).

L'équation différentielle ci-dessus montre que les solutions pour k quelconque sont homothétiques dans le rapport k des solutions pour k = 1, seul cas que nous examinerons ci-après.

Quelques cas particuliers :

     1) La courbe du filé est rectiligne.
 

Si l'on prend , le système différentiel cartésien du mouvement s'écrit , avec condition initiale : . L'équation différentielle polaire de la courbe s'écrit  (dérivée prise par rapport à q). Relation liant le rayon podaire p et l'abscisse : . Posant  et , on obtient successivement ,  (dérivée prise par rapport à t), , , d'où  Paramétrisation cartésienne dans le cas non homothétique : .

 

Dans le cas de tangente horizontale en O, la courbe ressemble à un kappa, mais l'équation ci-dessus montre que ce n'en est pas un.

Voici une image du réseau des solutions, limitées par la courbe bleue , qui est une campyle d'Eudoxe.

Lorsque le fileur a une position initiale à l'extérieur de la bande , il devient imaginaire lorsqu'il atteint la campyle d'Eudoxe (figure réalisée par Guy Valette).

Ce tracé de la partie réelle des solutions montre que le fileur ne fait en fait qu'une incursion momentanée dans le domaine imaginaire !

2) La courbe du filé est un cercle de centre O.
 

La courbe de filature n'est alors autre qu'un cercle passant par O, ou un cercle de centre O  dans le cas homothétique. On remarque bien ci-contre que l'on peut échanger fileur et filé. On remarquera aussi que la propriété mise en évidence est une simple application du théorème de l'angle au centre. Ce problème a reçu aussi l'habillage suivant : un homme court à vitesse constante le long du bord d'une arène ; un lion part du centre et poursuit l'homme, à même vitesse que lui, de sorte que tous deux soient alignés avec le centre ; quelle trajectoire suit-il, et en combien de temps rejoint-il l'homme ? cf. Ian Stewart, l'art de la fuite, in Visions géométriques, page 154.

 

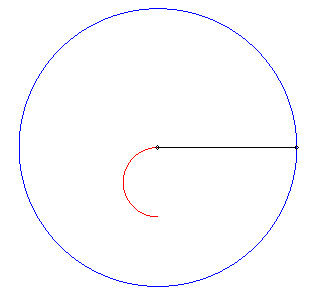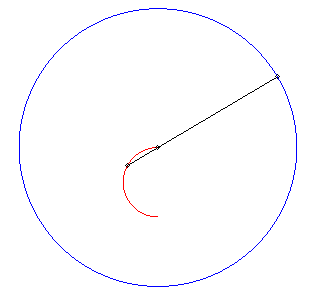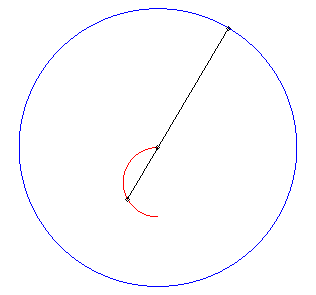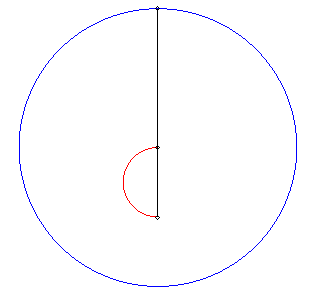Dans le cas précédent, le fileur rejoint le filé, alors que ce n'était pas le cas pour la droite ; mais même dans le cas d'une courbe bornée, il est possible que le fileur n'atteigne jamais le filé (et donc, avec l'habillage ci-dessus, que le lion n'atteigne jamais l'homme) ; par exemple, avec cette spirale ayant un cercle asymptote :

Contrairement aux apparences, ici, le lion (rouge) n'atteint jamais l'homme (bleu), bien que leur distance mutuelle tende vers 0.

Lorsque le point O est à l'infini, la courbe de filature devient la courbe de poursuite parallèle.

Voir aussi la courbe du crabe.
 
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2015