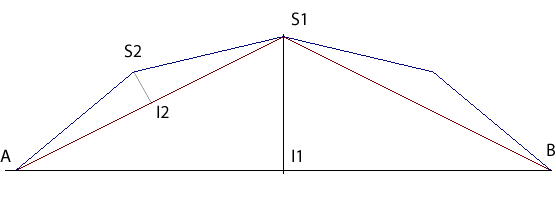
La courbe à flèches de base [AB]
est construite de la façon suivante : on construit sur [AB] un triangle
isocèle de sommet S1, sa hauteur
S1I1 (ici
nommée plutôt "flèche") étant dans un certain
rapport r1 à sa demi-base
AI1.
On effectue la même opération sur les deux
côtés, les flèches ayant le même rapport r2
à la demi-base.
Puis on effectue cette opération à l'infini
avec une suite des rapports flèche/demi-base égale à
(rn).
La courbe à flèches est la courbe
limite, si elle existe. |
 |
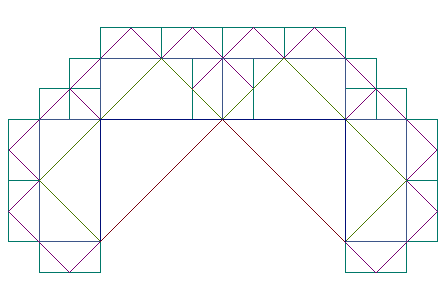
| Par exemple, si les rn
sont tous égaux à 1, la courbe obtenue n'est autre que le
fractal
de Lévy. |
|
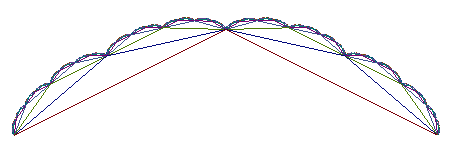
| Si les rn sont
tous égaux à r <1, on obtient toujours une courbe
fractale, attracteur de deux
contractions affines, dont la forme rappelle la courbe
du blanc-manger, de construction similaire. |
|
Mais cette méthode a été au départ
utilisée pour tracer, à l'aide de cordes, des raccordements
circulaires entre deux alignements.
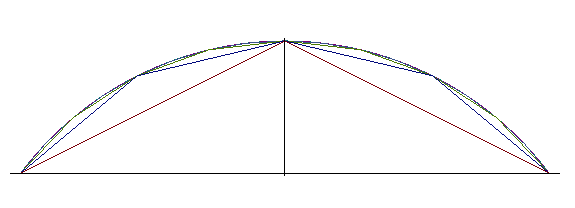
Une fois le sommet S1
choisi, un calcul montre que pour que les sommets Sn
se trouvent sur l'arc de cercle passant par A, S1,
B, il suffit de prendre 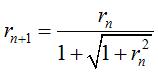 . .
La courbe limite est alors cet arc de cercle. |
|
Comme, dans la suite précédente, on a 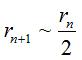 ,
si l'on prend ,
si l'on prend 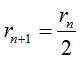 ,
on obtient une courbe très proche de l'arc de cercle. ,
on obtient une courbe très proche de l'arc de cercle. |
|
Si, dans le cas de l'arc de cercle, on note 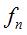 et
et 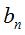 la
flèche et la demi-base à l'étape n, on a la
flèche et la demi-base à l'étape n, on a 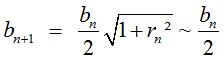 donc
donc 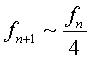 .
Si l'on construit donc une courbe à flèches où chaque
flèche est simplement le quart de la précédente
(ce qui donne .
Si l'on construit donc une courbe à flèches où chaque
flèche est simplement le quart de la précédente
(ce qui donne 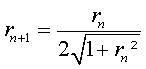 ),
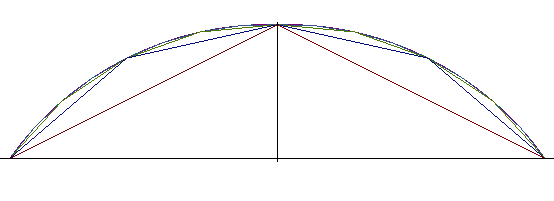
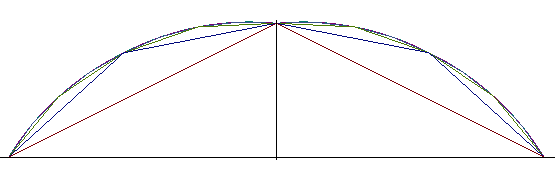
on obtient de nouveau une approximation de l'arc de cercle. C'est cette
courbe, de construction pratique simple, qui était désignée
par "courbe à flèches proportionnelles" dans les manuels
de construction de chemins de fer au 19ème siècle. ),
on obtient de nouveau une approximation de l'arc de cercle. C'est cette
courbe, de construction pratique simple, qui était désignée
par "courbe à flèches proportionnelles" dans les manuels
de construction de chemins de fer au 19ème siècle.
On constate ci-contre que l'approximation est moins bonne
que dans le cas précédent, mais le défaut s'atténue
avec un angle de départ plus petit. |
|





