COURBE DU BLANC-MANGER
Blancmange curve, Puddingkurve
| fractal suivant | fractal précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
COURBE DU BLANC-MANGER
Blancmange curve, Puddingkurve
| Courbe étudiée par Takagi
en 1903, et van
Der Waerden en 1930.
Le blanc-manger est une espèce de pouding au lait d'amandes ; la forme de la courbe rappelle en effet un pouding retourné. Autres noms : courbe de Takagi, courbe de van Der Waerden. Nom anglais : blancmange curve (nom donné par John
Mills) ;
|
Équation cartésienne : 
où d(x) est la distance de x à l'entier le
plus proche. |
La courbe du blanc-manger est la courbe de la fonction ci-dessus, introduite par Takagi pour donner un exemple de fonction continue dérivable en aucun point.
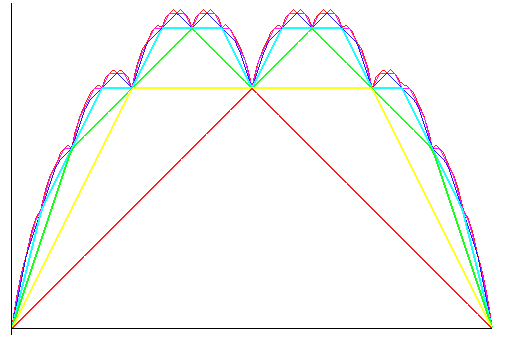
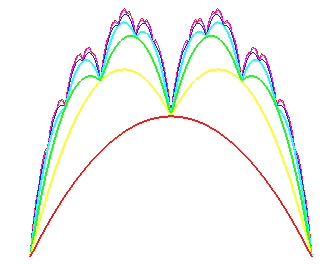
Ci-dessous à gauche les courbes des fonctions 
dont la somme donne la fonction bl (à droite) :
|
|
 |
Mais la relation 
montre que la courbe du blanc-manger B (pour x entre
0 et 1) est l'attracteur de la famille des
deux contractions affines f et g : 
et 
qui
sont des composées de transvection avec une homothétie de
rapport 1/2.
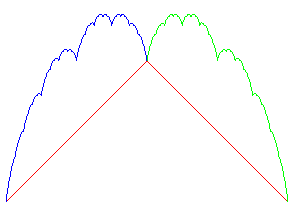
Vue montrant que  |
Vue montrant que 
;
on remarque que fg et gf sont des homothéties de rapport 1/4 |
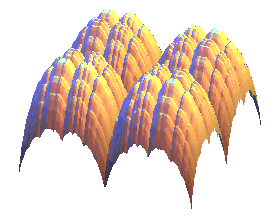
La surface
de translation engendrée par la translation d'une courbe du
blanc-manger le long d'une autre, perpendiculaire à la première,
d'équation 
,
est une élégante montagne fractale dénommée
"mont Takagi" :
Une variante : |
Une autre variante :  |
 
: on tombe sur une brave parabole y = 2 x (1- x) !
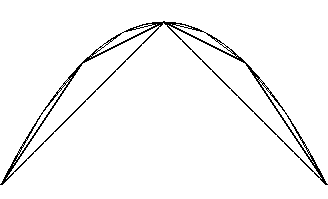Ceci constitue donc une construction approchée simple de cette parabole. |
 
avec  . |
Pour une autre courbe de fonction continue nulle part dérivable, voir la courbe de Bolzano.
Lire un intéressant article à : www.warwick.ac.uk/staff/David.Tall/pdfs/dot2000f-blancmange-english.pdf
| fractal suivant | fractal précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2013
