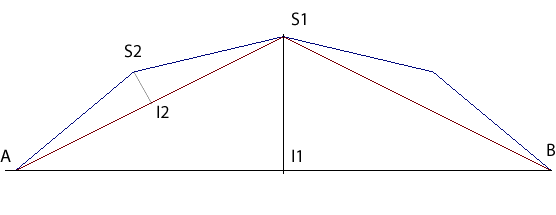
The sagittal curve with base [AB] is constructed
in the following way: an isosceles triangle with vertex S1
is drawn on [AB]. The ratio of its height S1I1
(rather called here the "sagitta") and the half-base AI1
is some number r1.
The same process is applied to both the other sides,
the sagittas having the same ratio r2
with respect to the half-base.
Then, this process is applied an infinite number of times
with the sequence of ratios sagitta/half-base (rn).
The sagittal curve is the limit curve, if it exists. |
 |
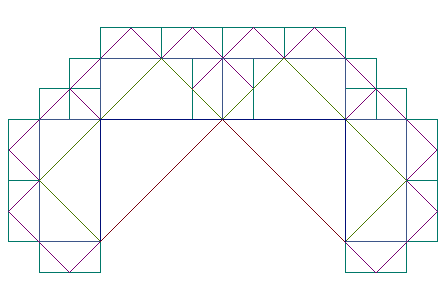
| For example, if the rn
are all equal to 1, then the resulting curve is none other than the Lévy
fractal. |
|
| If the rn
are all equal to r < 1, we still get a fractal, attractor
of two affine contractions, the shape of which reminds of the blancmange
curve, which has a similar construction. |
|
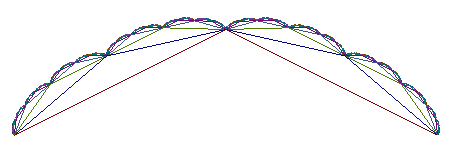
But this method was used, at first, to trace, thanks
to ropes, circular junctions between two lines.
Once the vertex S1 is
fixed, a calculation shows that for the vertices Sn
to be on the arc of a circle passing by A,S1,B,
one only has to take 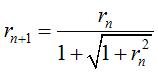 . .
The limit curve is then this arc of a circle. |
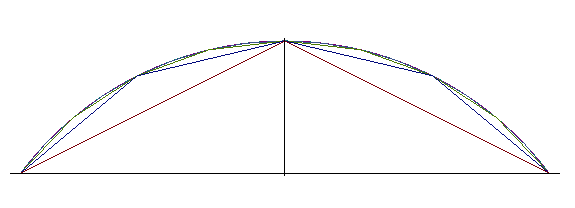
|
As, in the previous sequence, we have 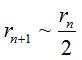 ,
if we take ,
if we take 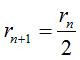 ,
we get a curve very close to the arc of a circle. ,
we get a curve very close to the arc of a circle. |
|
If, in the case of the arc of a circle, the sagitta and
the half-base at the step n are written respectively 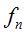 and
and 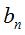 , then
we have , then
we have 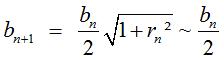 and so
and so 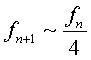 .
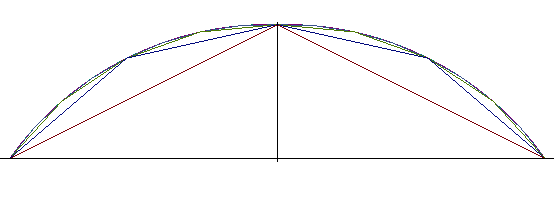
Therefore, if we construct a curve for which the sagitta is simply the
quarter of the previous one (which gives .
Therefore, if we construct a curve for which the sagitta is simply the
quarter of the previous one (which gives 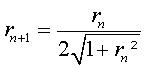 ),
we get again the approximation of the arc of a circle. It is this curve,
with a simple practical construction, that was referred to as "curve of
proportional sagittas" in the railway
construction manuals in the 19th century. ),
we get again the approximation of the arc of a circle. It is this curve,
with a simple practical construction, that was referred to as "curve of
proportional sagittas" in the railway
construction manuals in the 19th century.
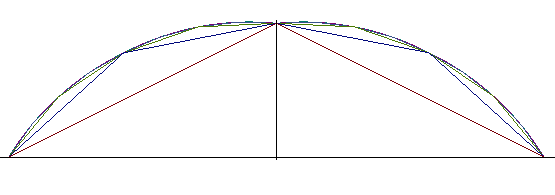
Note opposite that the approximation is far worse than
in the previous case, but the defect becomes less and less pronounced as
the initial angle is smaller. |
|





