,
la barycentrique est parcourue par M défini par 
.
En dérivant, on obtient
; la vitesse V de M, et la vitesse 
de ont
donc pour rapport 
.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
BARYCENTRIQUE
Barycentric
curve, Schwerpunktskurve
| Courbe étudiée par Cesàro en 1883, en 1886 (1) , en 1886 (2). |
| La courbe de départ étant parcourue par ,
la barycentrique est parcourue par M défini par .
En dérivant, on obtient
; la vitesse V de M, et la vitesse
de ont
donc pour rapport . |
|
La (courbe) barycentrique d’une courbe 
est le lieu des centres de gravité des arcs (homogènes) de
la courbe comptés à partir d’un point fixe.
La relation
montre que le vecteur vitesse du barycentre pointe toujours vers le point
de la courbe de départ, de sorte que la barycentrique est une courbe
de poursuite associée au mouvement du mobile de départ.
Exemples : la barycentrique de la droite est évidemment la même droite, la barycentrique du cercle est la cochléoïde.
Exemple détaillé :
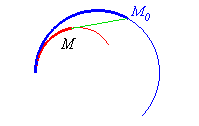
BARYCENTRIQUE DE LA SPIRALE
LOGARITHMIQUE, en partant de son point asymptote.
Pour la spirale de départ 
:
Paramétrisation cartésienne de la barycentrique :  .
Equation polaire dans un repère tourné d'un angle 
:  , où  . |
Barycentrique, en rouge, de la spirale bleue. |
La barycentrique de la spirale est donc une spirale égale.
De plus le rapport 
est égal à 
.
Étant constant, la barycentrique est donc une courbe
de poursuite classique.
© Robert FERRÉOL 2020