,
the barycentric curve is covered by M defined by 
.
By derivation we get
; the speed V of M, and the speed 
of
therefore have the ratio 
.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
BARYCENTRIC CURVE
| The starting curve being covered by ,
the barycentric curve is covered by M defined by .
By derivation we get
; the speed V of M, and the speed
of
therefore have the ratio . |
|
The barycentric curve of a curve (G0) is the locus of the gravity centers of the (homogenous) arcs of the curve, counted from a fixed point.
The relationship
shows that the velocity vector of the gravity center always points towards
the point of the starting curve, so that the barycentric curve is a pursuit
curve associated with the motion of the starting mobile.
Example: the cochleoid is the barycentric curve of the circle.
Detailed example:
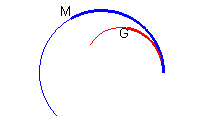
BARYCENTRIC CURVE OF THE LOGARITHMIC SPIRAL, starting
from its asymptote point.
For the starting spiral 
:
Cartesian parameterization of the barycentric curve :  .
Polar equation in a frame rotated by an angle 
:  , où  . |
Barycentrique, en rouge, de la spirale bleue. |
The barycentric curve of the spiral is therefore an equal
spiral. Moreover the ratio 
is equal to 
.
Being constant, the barycentric is therefore a classic pursuit
curve.
© Robert FERRÉOL 2025