Équation différentielle :  où a est le coefficient d'homotétie, et  ,  étant le coefficient d'élasticité relatif du fil (= 0 pour un fil inextensible) et   sa masse linéique au repos. Paramétrisation cartésienne :  ou   () Abscisse curviligne : . Rayon de courbure : . Courbe transcendante.

La chainette élastique est la forme prise par un fil pesant flexible infiniment mince homogène élastique suspendu entre deux points, placé dans un champ de pesanteur uniforme.
 

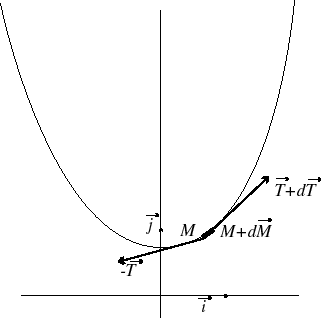
Comme pour la chainette ordinaire la relation de la statique donne, mais la densité linéique  n'est plus constante ; d'après la loi de Hooke elle est égale à   où l est le coefficient d'élasticité relatif du fil et  la densité au repos (l'allongement relatif du fil est proportionnel à sa tension). Cette relation s'intègre en  d'où  (1) ; elle montre aussi que la tension horizontale   d'où en dérivant (1) l'équation différentielle de la chaînette élastique :  soit, en posant  et : .

 
 

Cette équation, incomplète en x et en y,  s'écrit  qui s'intègre en  ou encore , qui s'intègre en , d'où la paramétrisation ci-dessus en prenant y' comme paramètre. Avec les notations ci-dessus, si le fil est obtenu pour , on calcule U implicitement par la relation  où  est la longueur du fil au repos, X l'abscisse du point où est accroché le fil, et P le poids du fil.

 

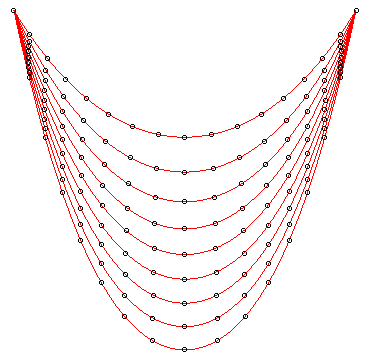
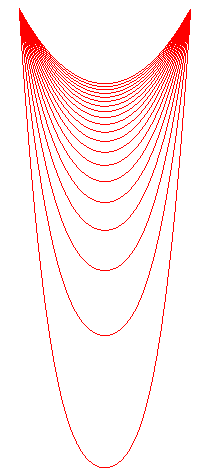
A gauche, animation montrant les diverses positions de la chainette élastique, pour un coefficient d'élasticité croissant en partant de 0, et pour un fil de masse fixée et de longueur au repos donnée. La courbe la plus haute est une chainette classique. On constate que l'allongement total est en gros proportionnel à l'élasticité. A droite, des positions équidistantes ont été marquées par des perles sur la chainette de départ ; on constate que la position horizontale reste à peu près constante lors de l'allongement.

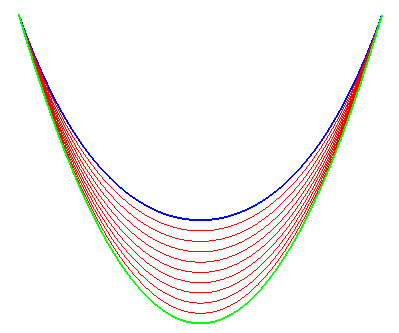
Si l'on oublie le problème physique de départ, en posant b=ka, on obtient les équations  qui donnent la chainette ordinaire pour b = 0, et la parabole x² = 2by pour a = 0. La chainette élastique fournit donc toutes les positions intermédiaires entre la chainette ordinaire et la parabole. Ci-contre, une illustration de ce fait (en bleu la chainette et en vert la parabole).

 

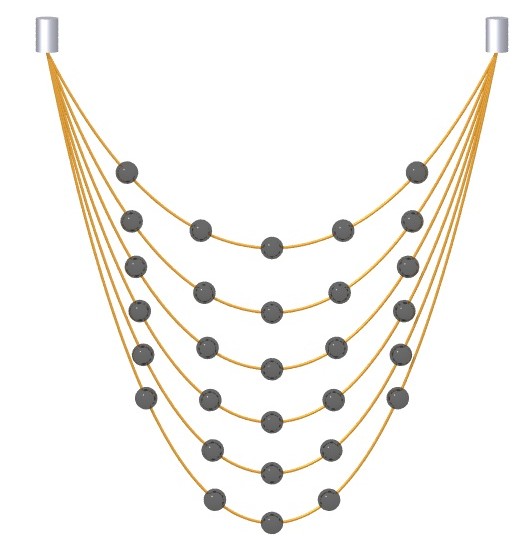
La manip expérimentale : les boulons étaient équidistants sur le fil élastique au repos.

Voir aussi la chainette d'égale résistance.
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2008