Elastic catenary

ELASTIC CATENARY

Production: Alain Esculier

Curve studied by Finck and Bobillier in 1826.

Differential equation:

where

, where

is the inverse of the elasticity coefficient of the wire (

= 0 for an inextensible wire) and

its linear mass density.
Cartesian parametrization:

(

)
Curvilinear abscissa:

.
Radius of curvature:

.
Transcendental curve.

The elastic catenary is the shape taken by an elastic, homogeneous, infinitely thin, flexible, massive wire hanging from two points, placed in a uniform gravitational field.

As for the ordinary catenary, the equations of electrostatics give, but the linear density is no longer constant; according to Hooke's law, it is equal to where l is the elasticicty coefficient of the wire and is the density at rest.
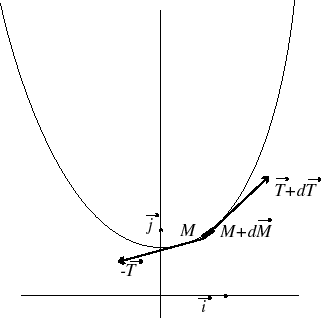It can be integrated to therefore (1); it also shows that the horizontal tension so that, by differentiating (1), we get the differential equation of the elastic catenary:
i.e., with and : .

This equation, with no x nor y, can be written as that can be integrated to , or as that can be integrated to , hence the above parametrization when y' is taken as a parameter.
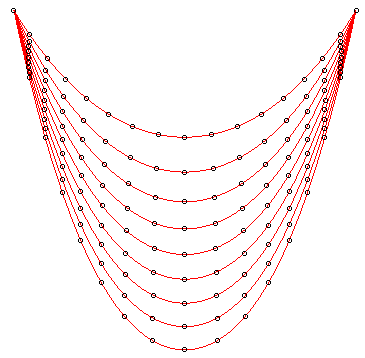
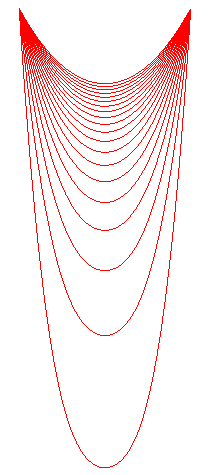
With the above notations, if the wire is described when u ranges between -U and U, the value of U can be implicitly calculated by the formula where is the length of the wire at rest, X is the abscissa of the point where the wire is attached, and P the weight of the wire.

On the left, an animation showing the various positions of the elastic catenary, for an elasticity coefficient growing from 0, and for a wire with fixed mass and given length at rest. The curve is higher than the classic catenary.
It can be noticed that the total extension is basically proportional to the elasticity.
On the right, equidistant positions have been marked by circles on the initial catenary. Note that the horizontal position stays approximately the same during the extension.

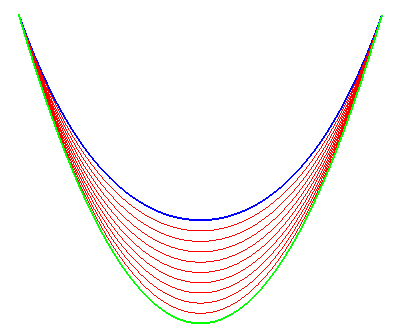
If we forget the initial physical problem, by setting b=ka, we obtain the equations which give the ordinary chain for b = 0, and the parabola x² = 2by for a = 0.
The elastic chain therefore provides all the positions intermediaries between the ordinary chain and the parabola.
Opposite, an illustration of this fact (the catenary is in blue and the parabola in green).

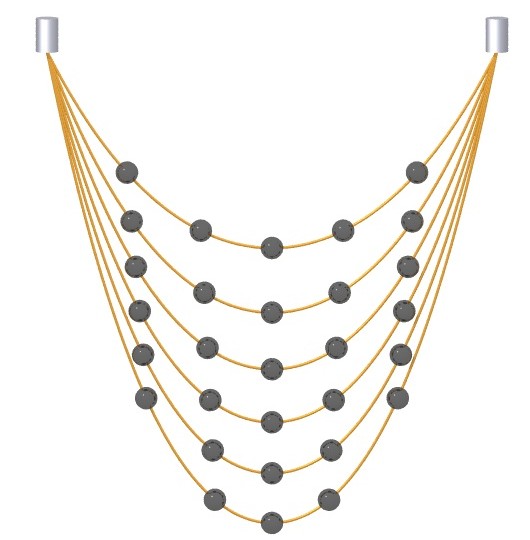
Experiment: the bolts were equidistant on the elastic wire at rest.

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra