où
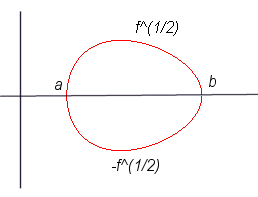
1) 
avec g strictement positive, C1
sur ]a, b[,
2) 
concave sur [a, b] .
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
Ovale
Oval,
Eikurve
| Du latin ovum "oeuf". |
Un ovale est une courbe plane ayant la forme d'un oeuf.
De façon très générale, on peut donner la définition : courbe de classe C1 frontière d'une partie convexe bornée du plan. Alors, une courbe fermée bornée de classe C1 dont tous les points ont une courbure positive est un ovale.
En se restreignant aux courbes ayant un axe de symétrie,
on peut donner l'équation :
| Équation cratésienne :
où
1) 2) |
|
Exemples rentrant dans cette définition :
l'ellipse ( ,
k étant le coefficient d'applatissement), ci-contre avec k
= 3/4 |
 |
L'ovale de Tolstoï ( ),
cas particulier d'ovale de Cassini |
 |
le folium simple
( , a
= 0, b = 1) |
 |
un demi oeuf
double ( ,
a = 0, b = 1) |
 |
l'ovale de l'hyperbole
cubique à ovale (
, 0 < a < b ), ci-contre avec a = 1, b
= 2, k = 3/4 |
 |
l'oeuf de Granville
( , 0 < a
< b) , ci-contre avec a = 4, b = 6, k =
4 |
 |
la courbe de Rosillo
( ,
b = –
a, a < c < d ), ci-contre avec a = 1,
c
=
2, d = 3 |
 |
Voir aussi les ovales de Descartes, les oeufs d'Ehrhart, les courbes de la bielle de Bérard, les foliums droits, les ovoïdes obtenus par révolution d'un ovale.
Pour un répertoire des courbes en forme d'oeuf
: www.mathematische-basteleien.de/eggcurves.htm
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2024