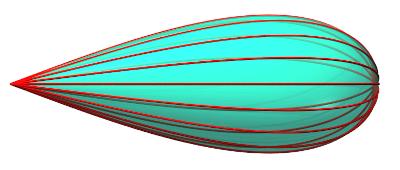
Tannery's pear

TANNERY'S PEAR

Surface discovered by Tannery in 1892 (bulletin des sciences mathematiques, page 190).
Jules Tannery (1848 - 1910): French mathematician.

Cartesian parametrization: ().
Cylindrical equation: .
First quadratic fundamental form :
Equation of a geodesic given by .

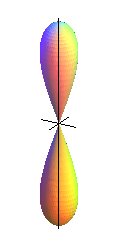Tannery's pear is the surface of revolution generated by the rotation around its axis of a half-lemniscate of Gerono subject to a scaling in one direction with ratio (the rotation of the entire figure-eight is sometimes called Tannery's hourglass).

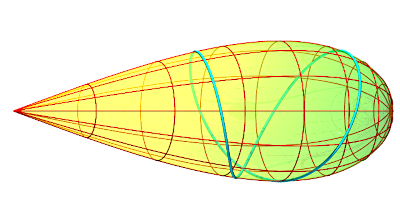
It is remarkable that the geodesics of this surface are closed, shaped like a curved figure-eight, except for the meridians (the surfaces for which the geodesics are closed are called "Zoll surfaces").
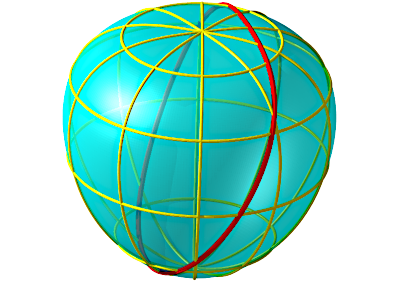
Moreover, the equation above proves that they are algebraic curves, and Tannery proved that they all have the same length (and therefore the length of a meridian and the double of the length of the parallel with maximal length that is also a geodesic).

En 1903, Otto Zoll determined asurface of which all geodesics are closed and of same length, other than a sphere, and that is smooth, contrary to the Tannery's pear :
Cartesian parametrization : ().
First fundamental quadratic form : .

next surface previous surface 2D curves 3D curves surfaces fractals polyhedra