ROMAN SURFACE

| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
ROMAN SURFACE


| Surface studied by Steiner in 1844.
This surface was named this way by Steiner because he discovered during a stay in Rome. |
| Cartesian equation as a tetrahedral surface of Kümmer: so that f = 0 is the equation of the sphere with center O and radius a and pqrs = 0 is the equation of a regular tetrahedron centered on O and the edges of which are at distance a from O. Cartesian equation in a frame turned by 45° around Oz: Cartesian parametrization: i.e., by taking i.e. by taking One-sided quartic surface, special case of Steiner surface. |
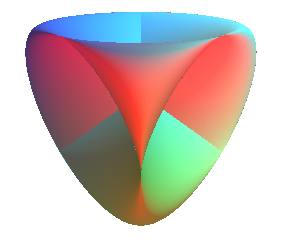
The Roman surface is the image of the quotient of the sphere(center O
O, radius 1) by the antipodal relation (in other words the real projective plane) by the map: .
It is historically the first representation of the projective plane as a surface in .
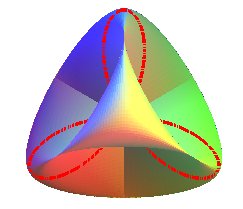
It has three segment lines of self-intersection that form a right trihedron each of them ended by two cuspidal points and intersecting at their center in a triple point (here O).
The above definition as a special case of Kummer surface shows that it has the symmetries of the regular tetrahedron.
With the second equation, the vertices of the tetrahedron are the points , with an even number of minus signs.
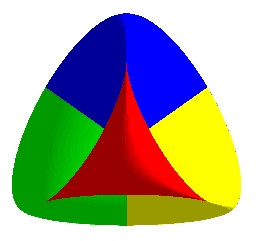

| The Roman surface is, in three ways, the union of ellipses (with the second equation above, they are the sections by the planes containing the axes); we could say that the Roman surface, in the manner of the cross-cap, is a triply "ellipsed" surface.
Opposite, the family of ellipses located in the planes passing by the vertical double line. |
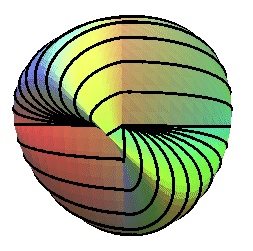 |
| The sections by the planes perpendicular to the axes of rotation of order 3 form the family of hypotrochoids with 3 branches.
In particular, the section by the central plane is the regular trifolium. |
 |
| The sections by the planes perpendicular to the double lines are the lemniscates of Booth. | 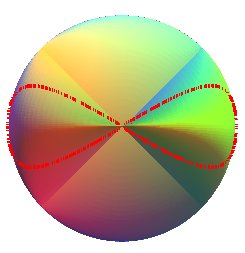 |
| Finally, here is a polyhedral version of the Roman surface: | an another one, where the cubes were truncated in orthocentric tetrahedra: |
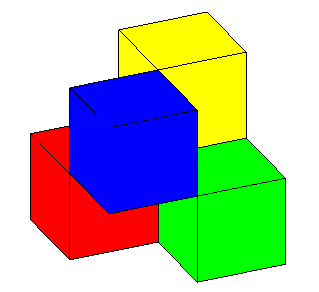 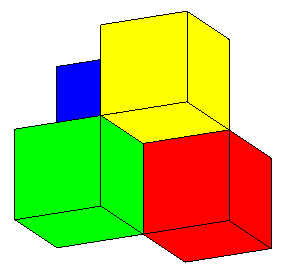
Find the 3 double segment lines ended by the 6 pinch points, the 4 vertices, and the triple point! |
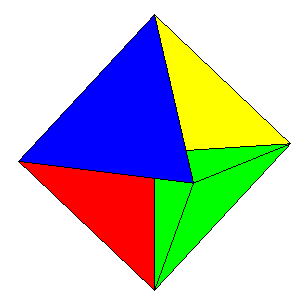 |
| Attention 1: if you see hollow cubes, you are victim of an illusion!
Attention 2: it is not a true polyhedron: the double edges are common to 4 faces. |
Here neither, it is not a polyhedron but the central faces are united into 4 squares, we get a crossed polyhedron, that is even semiregular, called tetrahemihexahedron. |
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL , Jacques MANDONNET 2017