Curves studied by Lamé in 1818. Gabriel Lamé (1795-1870): French mathematician and engineer. Other names for >2: super-ellipse, super-circle (if a = b), squircle (contraction of the words square and circle).

 

Cartesian equation of :  ;  :  with a, b > 0 , ;  Cartesian parametrization of  : . Area delimited by  :  where  , i.e.  if .

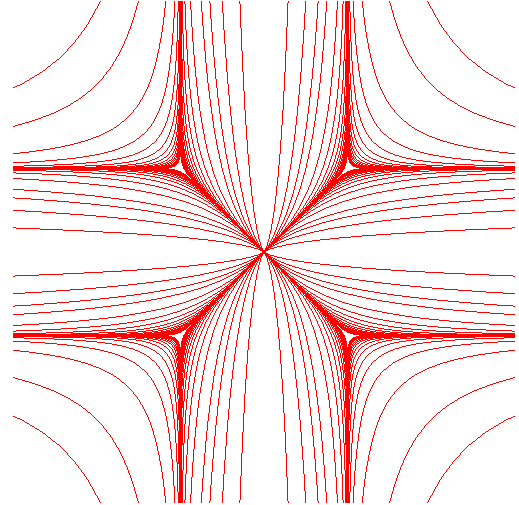
The Lamé curves  and  are defined by their Cartesian equation above.
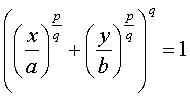
For rational values of , the curve , the part of  located in the  quadrant, is a portion of an algebraic curve  of degree pq ?, and equation  ? (when p is even,  and  coincide); the same holds for the curves .

Examples of curves with a = b:
 
 

	Lamé curve	associated algebraic curve	figure: the Lamé curve in red, the associated algebraic curve in green.
1	square:	line:
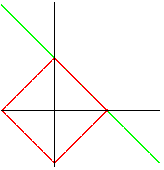2	circle:	ditto
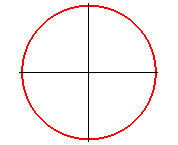3		Lamé cubic:
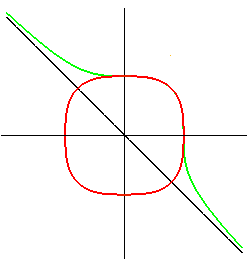1/2	union of 4 arcs of parabolas:	parabola:
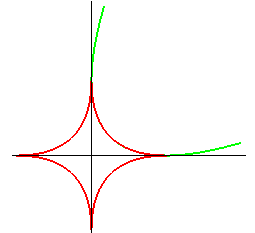2/3	astroid:	ditto
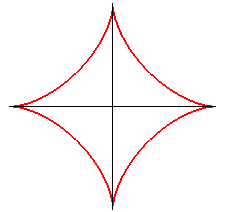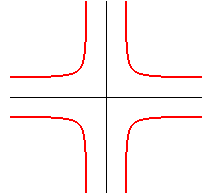
- 1	union of 4 branches of rectangular hyperbolas:	rectangular hyperbola:
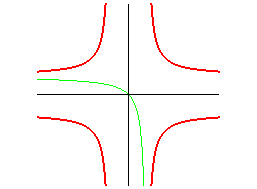-2	crosscurve:	ditto

 
 

	Lamé curve	associated algebraic curve	figure: Lamé curve in red, the associated algebraic curve in green.
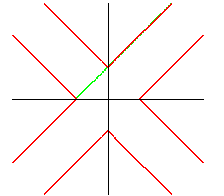
1	eight half-lines:	line:
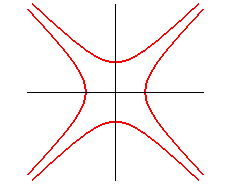
2		rectangular hyperbola:
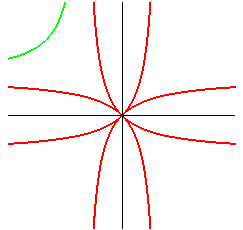
1/2	union of 8 arcs of parabolas:	parabola:
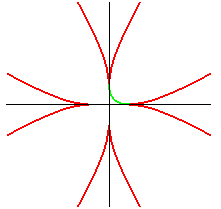2/3	and its symmetric image about y = x, of equation	ditto; it is the union of two evolutes of hyperbola.
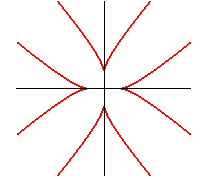
- 1	union of 8 branches of rectangular hyperbolas:	rectangular hyperbola:
-2		bullet nose curve:

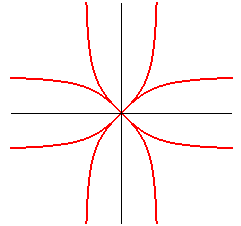When a = b =1 and a  = n is an integer,  is the Fermat curve.

See also the Lamé surfaces.

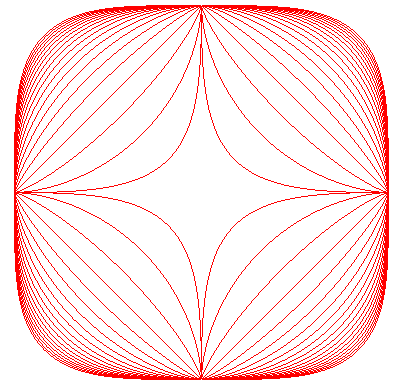
next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL 2017