Notion étudiée par Réaumur en 1709 et Lancret en 1811. Autre nom : développée oblique. Voir Aoust p. 77,  Bouasse p. 450 , Loria p. 297. Voir aussi cette thèse.

 

Pour une courbe de départ :  de point courant  la développoïde est l'ensemble des points . Paramétrisation complexe : . Si la courbe de départ a pour équation intrinsèque 2 : , on obtient : Équation intrinsèque 1 paramétrique : . Équation intrinsèque 2 :.

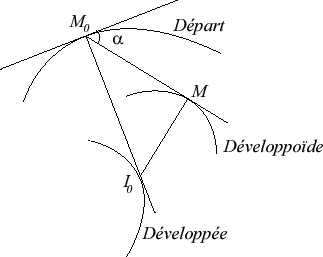
Les développoïdes d’une courbe (G) sont les enveloppes des droites (D) faisant un angle constant a avec la courbe de départ ; lorsque a = p/2, on retrouve la développée, et lorsque a est nul ou plat, on retrouve la courbe elle-même.
Le point caractéristique de l'enveloppe se construit très simplement par projection du centre de courbure de la courbe de départ sur la droite (D) (théorème de Réaumur).

Exemples :
    - la développoïde d'une droite est le point à l'infini de la droite variable.
    - les développoïdes d'un cercle sont des cercles concentriques :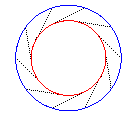 
    - les développoïdes d'une spirale logarithmique sont des spirales logarithmiques.
    - Les développoïdes d'une courbe cycloïdale (équation intrinsèque ) sont  semblables à la courbe de départ (équation intrinsèque avec ).
 

Les développoïdes de la cycloïde sont des cycloïdes isométriques. Ci-dessous, la développoïde à 45°.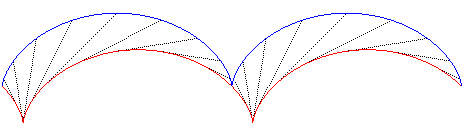

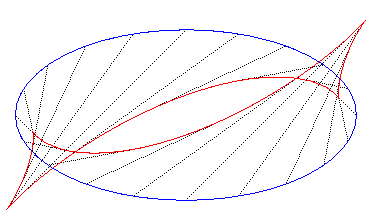
Ci-dessous, la développoïde à 60° d'une cardioïde.

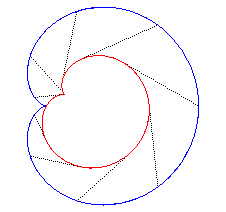courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2007