Contrairement aux lignes géométriques, comme les lignes de courbure, asymptotiques et géodésiques, qui sont intrinsèques à la surface, les lignes topographiques d'une surface sont des lignes dont la définition est associée à une direction, dite verticale ; on définit en particulier les lignes de niveau, de plus grande pente, de pente constante (hélices), d'angle constant avec les lignes de niveau (loxodromies), de déclivité extrémale, de talweg et de crête, d'écoulement.
 

Exemples (en rouge les crêtes, en bleu les talwegs) :
 

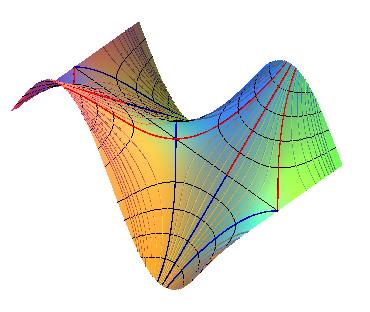
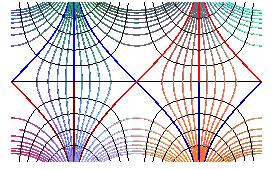
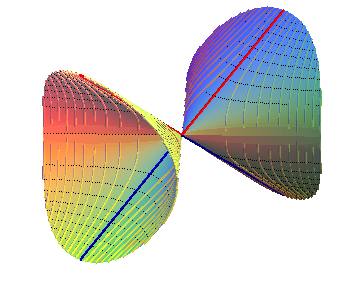
Paraboloïde hyperbolique : xy = z. Projections horizontales des lignes de niveau : hyperboles xy = cte. Projections horizontales des lignes de pente : hyperboles x2 - y2 = k (tournées de 45° par rapport aux précédentes). (écrire ) Talweg (bleu) : y = -x. Crête (rouge) : y = x.
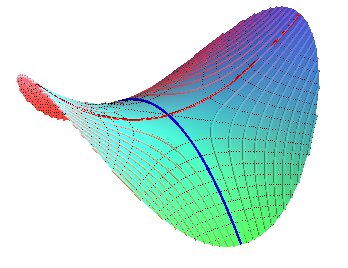
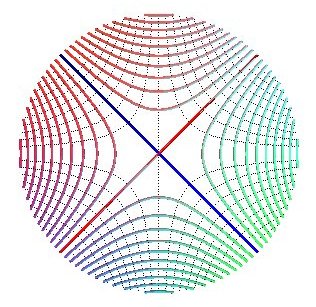
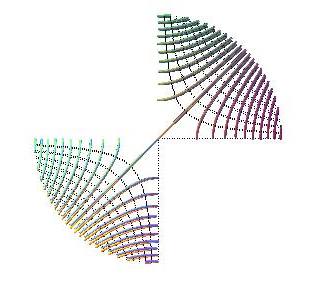
Cône elliptique : xy = z2. Projections des lignes de niveau : portions des hyperboles xy = k. Projection des lignes de pente : portions des hyperboles x2 - y2 = k . Remarque : les projections des lignes de niveau et de pente sont, dans le domaine xy >0, les mêmes que celles de la surface précédente, ce qui montrent que les projections des lignes de niveau et de pente ne sont pas caractéristiques de la surface.
Paraboloïde elliptique : x2 /2 + y2  = - z. Projections des lignes de niveau :  ellipses x2 /2 + y2  = k. Projection des lignes de pente :  paraboles y = k x2  plus x = 0. (écrire ) Les lignes de pentes singulières (en rouge) sont x = 0 et y = 0 mais seule la deuxième est ligne de crête.
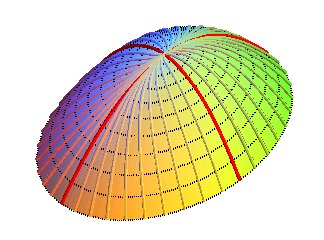
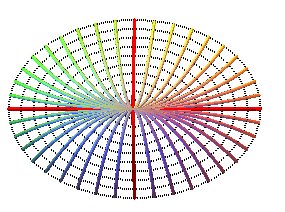
Cône elliptique : x2  = zy. Projection des lignes de niveau : paraboles cte.y =  x2.  Projections des lignes de pente : ellipses x2 /2 + y2  = k. Niveau et pente s'échangent avec la surface précédente !
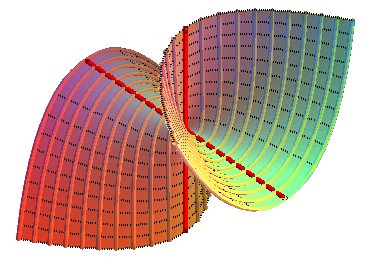
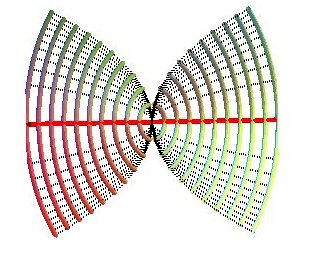
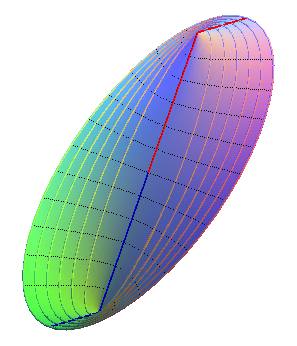
Surface d'équation : - z = PA + PB, où P est le projeté de M sur xOy. Projections des lignes de niveau : ellipses de foyers A et B. Projections des lignes de pente : hyperboles de foyers A et B.
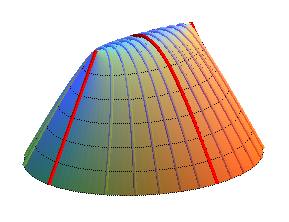
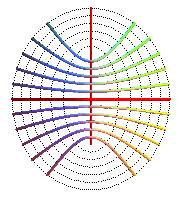
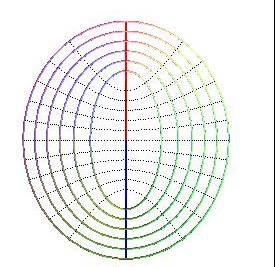
Surface d'équation : z = PA -PB, où P est le projeté de M sur xOy. Projections des lignes de niveau : hyperbole de foyers A et B. Projections des lignes de niveau : hyperboles de foyers A et B. Il ya donc de nouveau échange niveau-pente avec la surface précédente.
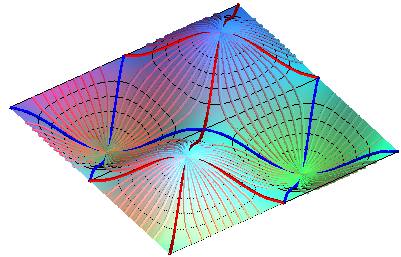
Boîte à oeufs : z = sin x sin y. Projections de lignes de niveau :  sin x sin y = k.   Projections des lignes de pente :  cos x = k cos y. (écrire )
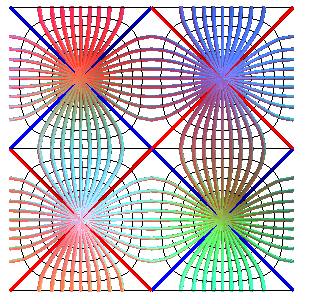
Surface z = y sin x. Projections des lignes de niveau : les sécantoïdes : y = k/sin(x). Projections des lignes de pente :  exp(y²) cos² x = k. () Lignes de pente singulières : cos x = 0. Les lignes de pente passant par les cols : exp(y²) cos² x = 1 ne sont pas des lignes de pente singulières...

 
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL , Jacques MANDONNET 2009