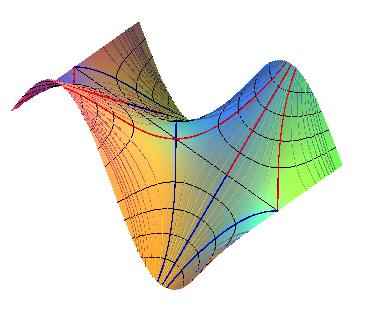
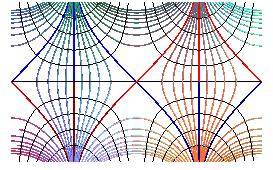
Horizontal projections of the contour lines: hyperbolas xy = constant.
Horizontal projections of the slope lines: hyperbolas
x2
- y2 = k
(turned by 45° with respect to the previous ones).
(write )
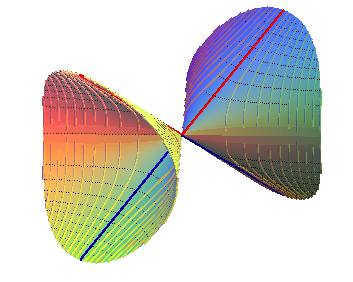
Thalweg (blue): y = -x.
Crest (red): y = x.
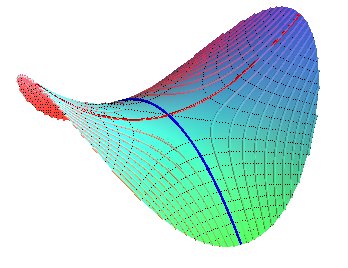
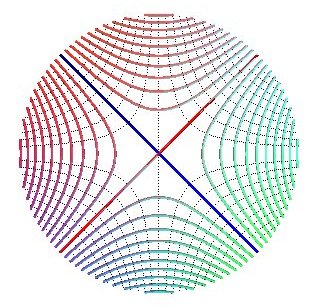
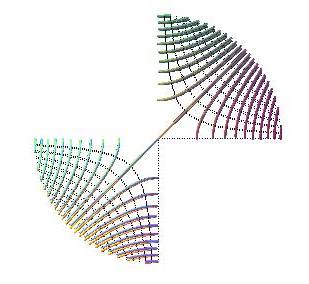
Projections of the contour lines: portions of the hyperbolas xy = k.
Projections of the slope lines: portions of the hyperbolas x2 - y2 = k .
Remark: the projections of the contour and slope lines are, in the domain xy >0, the same as those of the previous surface, which proves that the projections of the contour and slope lines cannot characterize the surface.
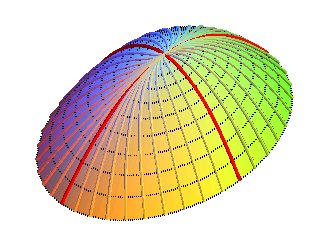
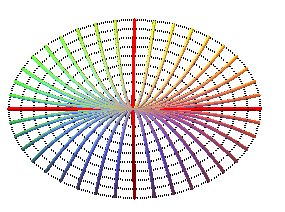
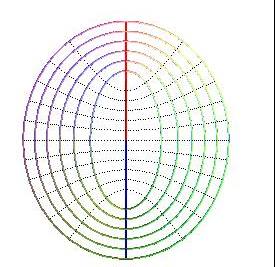
Projections of the contour lines:
ellipses x2
/2 + y2
= k.
Projections of the slope lines:
parabolas y = k x2
and x = 0.
(write )
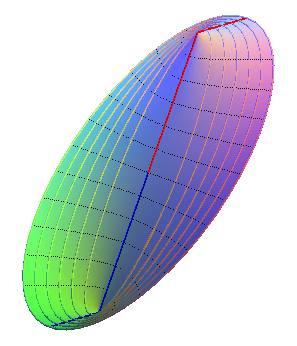
The singular slope lines (in red) are x
=
0 and y = 0 but only the latter is a crest line.
Projections of the contour lines: parabolas constant.y = x2.
Projections of the slope lines: ellipses x2 /2 + y2 = k.
Contour and slope lines are swapped in comparison with the previous surface!
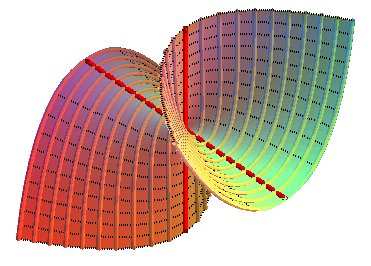
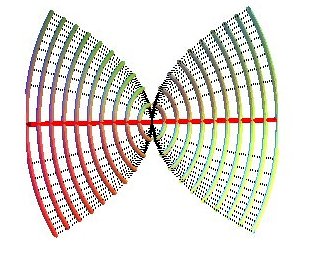
Projections of the contour lines: ellipses with foci A and B.
Projections of the slope lines: hyperbolas with foci A and B.
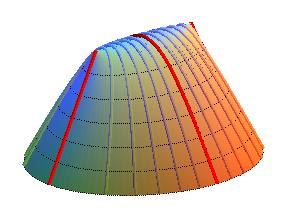
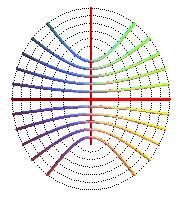
Projections of the contour lines: hyperbola with foci A and B.
Projections on the contour lines: hyperbolas of foci A and B.
Again, there is a swap contour/slope lines in comparison with the previous surface.
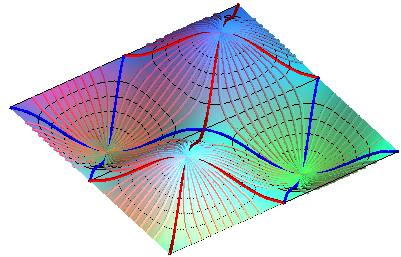
Projections of the contour lines:
sin x sin y = k.
Projections of the slope lines:
cos x = k cos y.
(write )
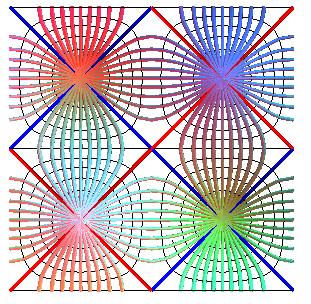
Projections of the contour lines: the secantoids: y = k/sin(x).
Projections of the slope lines:
exp(y²) cos² x = k.
()
Lines with singular slope: cos x = 0.
The slope lines passing by the saddles: exp(y²) cos² x = 1 are not singular slope lines...