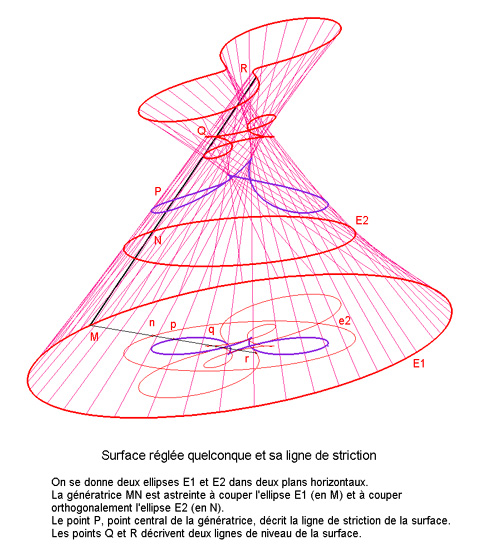
STRICTION LINE OF A NON DEVELOPABLE RULED SURFACE
The striction line of a non developable
ruled surface is the
locus of the central points (or striction points) of each
non parabolic generatrix of the surface; these points are
- the points where the tangent plane
is perpendicular to the asymptotic plane (i.e. the limit of the tangent
plane when it goes to infinity along the generatrix), or,
- the points where the absolute value
of the total curvature along a generatrix has a maximum (see the above
Lamarle formula), or even
- the limit points of the common perpendicular
to the generatrix and another generatrix that approaches it.
The latter definition also works in the case where the
surface is developable, and the resulting line is none other than the cuspidal
edge of this surface.
The striction line is not necessarily perpendicular to
the generatrices (the condition is the orthogonality of M1'
and a', not that of M1'
and a). However, it contains (locally?) singular points of the surface.
When the surface is ruled and has a directrix
plane, the projection on the striction line of the directrix plane
is the envelope of the projections of the generatrices.
Examples:
- the striction line of a conoid
is its axis in the right case, but not necessarily in the oblique case,
- the striction line of a one-sheeted
hyperboloid is its bore circle when it is of revolution, but not in
the general case,
- the striction line of a ruled
helicoid is its bore helix,
- the striction line of the hyperbolic
paraboloid,
- the striction line of the Möbius
surface,
- the striction line of the milk
carton.
Some illustrations of these notions, by Robert March.
References: (Mir
p.64, 67) (Deltheil p.251) (Bouasse p. 514)
© Robert FERRÉOL
, Robert MARCH 2018
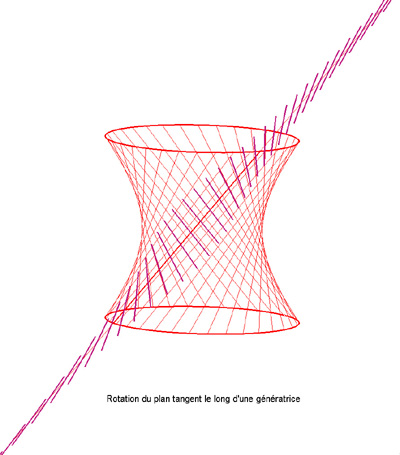
can be geometrically interpreted by the formula
,
where
is the angle between the tangent plane at C and the tangent plane
at M (Chasles rule); in an equivalent fashion, the surface generated
by the normals along the generatrix is a rectangular
hyperbolic paraboloid with cylindrical equation
in a frame Cxyz, Cz being the generatrix.
.