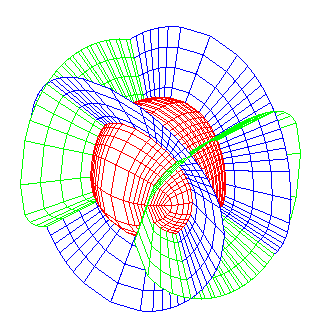
Family of elliptic cones that draw on the sphere a double orthogonal system of biquadratics; see at triple orthogonal system.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
BIQUADRATIC CURVE
| Other name: 3D quartic curve of the first kind. |
Biquadratics are algebraic curves of degree four that are the intersection between two quadrics that do not share a common line (in which case the curve would be of degree three).
It can be proved that all the biquadratics can be obtained as the intersection between two cones or cylinders of degree 2 (Poncelet theorem). In the case of two cylinders of revolution, the curve is said to be bicylindrical.
If one of the quadrics is a sphere, then the curve is called spherical biquadratic, or spherical cyclic curve, and can always be obtained as the intersection between a sphere and a cylinder or cone of degree 2 (Poncelet theorem again); examples: the spherocylindrical curves (including the Viviani curve), the spherical ellipses, a special case of spherical cycloid, and another example on the page seam line of a tennis ball.
Other example: the pancake curve, intersection between a cylinder of revolution and a parabolic cylinder.
See also Cartesian ovals, Booth curves (including the lemniscate of Bernoulli), the Külp quartic, the Dürer shell curve, the bicorn, that are planar projections of biquadratics.

| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2018