Spherical cycloid

SPHERICAL CYCLOID

Curve studied by Jean Bernoulli in 1732, and later by Hachette in 1811, and by Reuleaux.

Cartesian parametrization: .
Spherical curve, algebraic iff q is rational (degree = 2(numerator + denominator of q)).

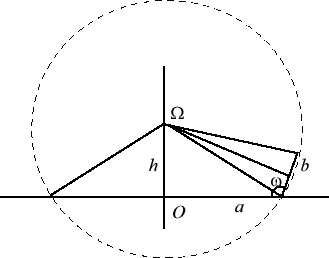
A spherical cycloid is the locus of a point on a circle rolling without slipping on a fixed circle, the angle between the two circles remaining constant equal to ; here, a is the radius of the fixed circle, that of the moving circle, and xOy the plane where lies the fixed circle.

When = 0, we get the hypocycloid, and when = , the epicycloid; apart from these two cases, the cycloid is traced on the sphere corresponding to both the base and the rolling circles, hence its name of spherical cycloid. The center W of this sphere is the point on Oz at height and its radius is .
Therefore, the spherical cycloid is a roulette of the motion of a sphere over a sphere.

Therefore, except in degenerate cases, the spherical cycloid is also the locus of a point on a cone of revolution that is rolling without slipping on a cone of revolution with the same vertex: these two cones are the cones with vertex W that contain the fixed circle and the moving circle, respectively.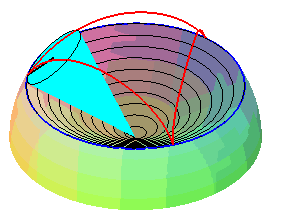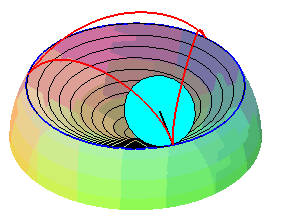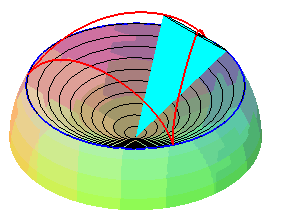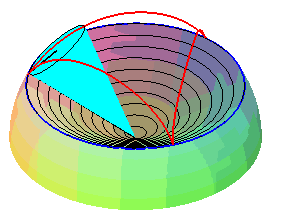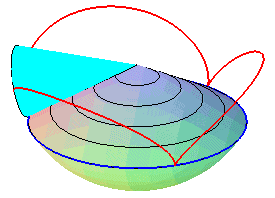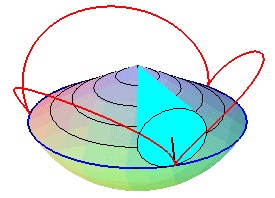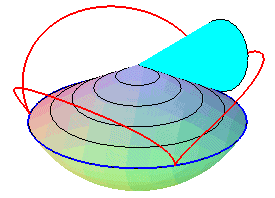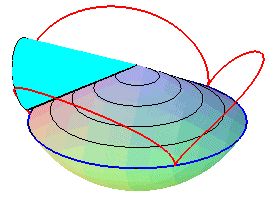

If q is rational, then the spherical cycloids are composed of a number of isometric arches equal to the numerator of q. If q is irrational, then they are composed of an infinite number of isometric arches.
The arches meet at cuspidal points, obtained for , located on the rolling circle, at altitude 0, and their vertices are located on the circle at altitude , with radius .

When and , i.e. , the radius of the circle passing through the vertices is less than or equal to the radius of the base circle. In this case, the curve is referred to as a spherical hypocycloid.
When and , i.e. , or when , the radius of the circle passing through the vertices is greater than or equal to the radius of the base circle. In this case, the curve is referred to as a spherical epicycloid.
In the intermediate case , these two circles have the same radius and the curve is a spherical helix. In this case, the vertices are also cusps, the center of the moving circle is W (it is therefore a great circle of the sphere) and rolls without slipping on the circle passing through the vertices, and the above rolling cone degenerates into a plane.
If we change q into q/(q + 1) and 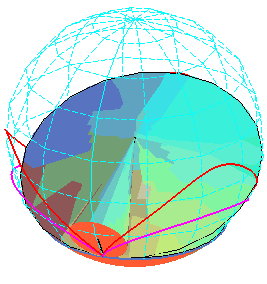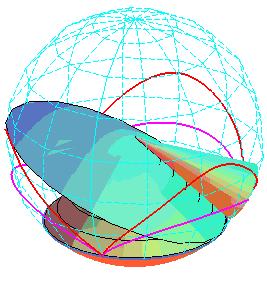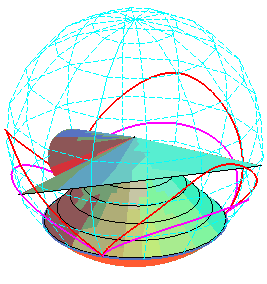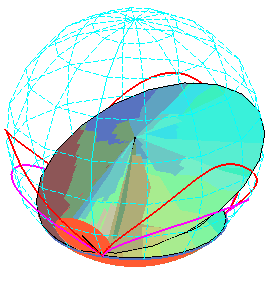into , then the curves look the same and the circles passing through the vertices have the same altitude, but are not equal: contrary to the case of plane epi- and hypocycloid, there is no double generation.

case : hypocycloid

case : epicycloid case : epicycloid

case : spherical helix.

case in red, and in blue.

In this animation, the circles passing by the vertices of the two cycloids have the same radius, but not the same altitude.

Special case q = 1 (base and rolling circles with equal radii) :

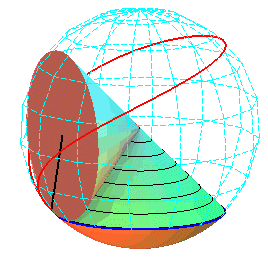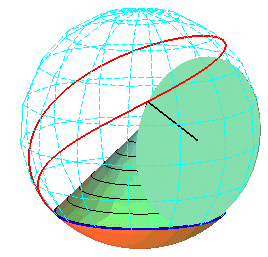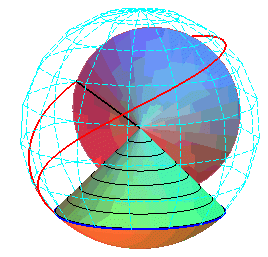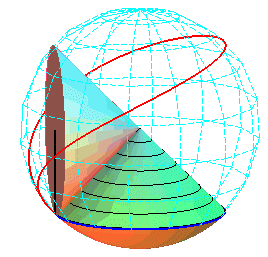
Cartesian parametrization:

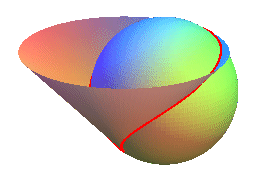
The projections on xOy, yOz, xOz are a cardioid, an arch of a parabola and a piriform quartic, respectively.

The curve is the intersection between the sphere and the cone of revolution tangent at its vertex to the sphere ; therefore, it is a spherical biquadratic.

The superb models below show the generation of spherical cycloids by the rolling motion of a cone on another cone.

Each point of the wheels of these bikes describes a spherical epicycloid.

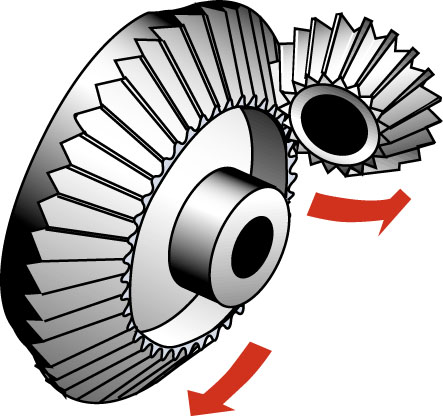The relative movements of the conical gears describe spherical epicycloids.

See the generalization to spherical trochoids.

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra