System of Cartesian equations:
Biquadratic.
Cartesian parametrization:
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
SPHERO-CYLINDRICAL CURVE
| Other name: cyclo-cylindrical curve. |
The sphero-cylindrical curves are the intersections
between a sphere and a cylinder of revolution.
| For a sphere centered on O with radius a,
a cylinder with radius b, and axis at distance c from O:
System of Cartesian equations: Biquadratic. Cartesian parametrization: |
Case :
| The curve is not empty iff Opposite, the case a = b = c. |
 |
Case b < a;
b + c < a: the curve has two
components
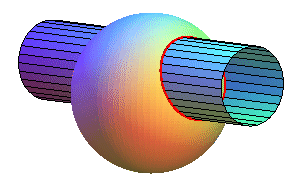 |
b + c = a: eight-like curve called hippopede.  |
a – b < c 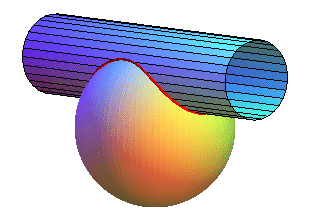 |
| It can be generalized by the intersection of the sphere and an elliptic cylinder, that is a spherical ellipse when the axes of the cylinder goes through the center of the sphere. | 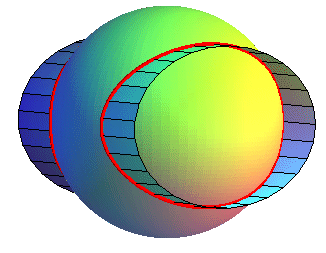 |
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2022