Bicylindrical curve

BICYLINDRICAL CURVE

The bicylindrical curves are the intersections between two cylinders of revolution.

First case : two orthogonal cylinders with radii a and b, and axis at distance 2c.

System of Cartesian equations:.
Biquadratic.
Cartesian parametrization: .
Cartesian equation of the projection on xOy: (see the Alain curve).
Area of the portion of cylinder delimited by each component, for and c = 0, given by an elliptic integral of the second kind: , that reduces to 4a² when a = b.

Case a = b:
The curve is invariant under the two half-turns that swap the two cylinders.

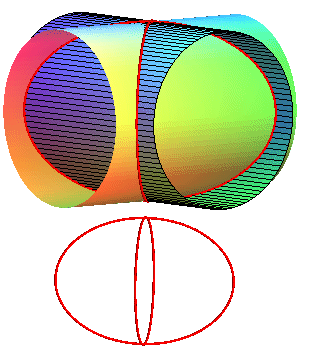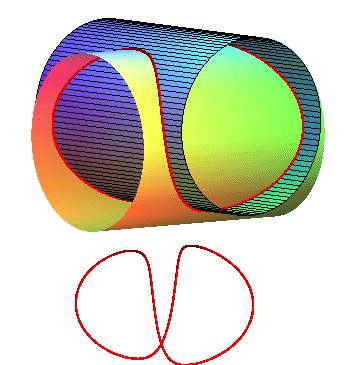
c = 0: it is the reunion of two ellipses with eccentricity that intersect at their secondary vertices with a right angle.

Small c.

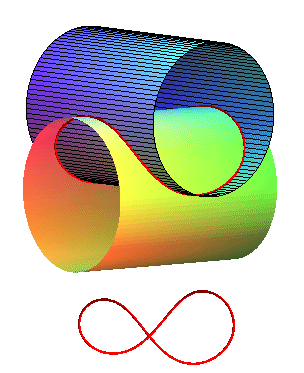
c = a /2

Case a < b:

(here c = 0): curve with two components.
: figure-eight curve similar to the hippopede.
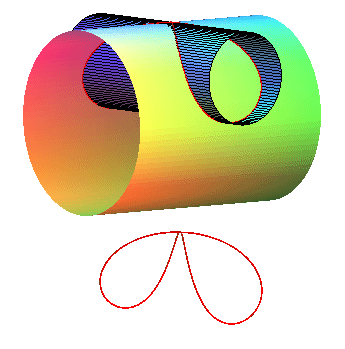See the Alain curve. : curve with one component.

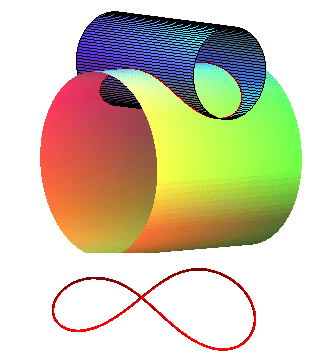One can notice that the bicylindrical curve is traced on the ellipsoid .
By scaling, we can turn the ellipsoid into a sphere, while the two cylinders become elliptic cylinders. The intersection obtained is one of the possible seam lines of a tennis ball.

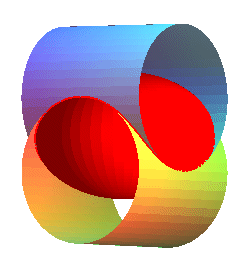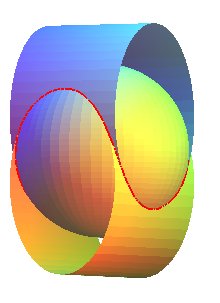Coiling the iso-energy curves of the pendulum leads to bicylindrical curves that are the intersection between cylinders with perpendicular axes.

Second case : two cylinders with secant axes, one of radius a, the other of radius b, forming an angle with the plane orthogonal to the first.

System of Cartesian equations: .
Cartesian parametrization: , where .
Case a = b : , union of two ellipses. Case a = b

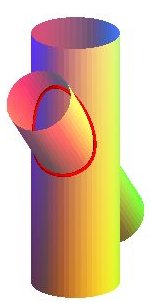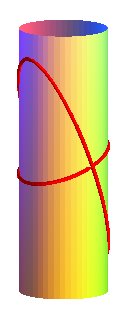The Swiss jeweler Philippe Mingard uses bicylindrical curves for his creations (case a = b, small c); he believes that this curve is "the manifestation of simplicity and purity incarnate".
See also the case of the seam line of a tennis ball, or the pancake curve, other curves that are invariant under a half-turn.

The Ulysse Lacoste rulpidon, a Steinmetz solid pierced with two full cylinders, reveals 10 edges which are 5 bicylindrical curves one of which is formed by two ellipses.

Beams of my chalet...
Botzaris station, in the Parisian Metro.
Lights in my staircase

Many other examples on the mathourist's page!

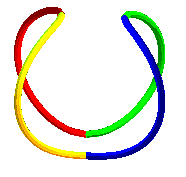
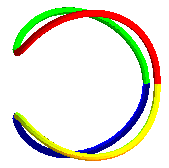
next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

The Swiss jeweler Philippe Mingard uses bicylindrical curves for his creations (case a = b, small c); he believes that this curve is "the manifestation of simplicity and purity incarnate". See also the case of the seam line of a tennis ball, or the pancake curve, other curves that are invariant under a half-turn.
The Ulysse Lacoste rulpidon, a Steinmetz solid pierced with two full cylinders, reveals 10 edges which are 5 bicylindrical curves one of which is formed by two ellipses.