Curve studied by Johannes Bernoulli in 1742 (Opera, T IV, p. 248). Homemade name ; other names : spiral of the hyperbolic cosine, spiral of the hyperbolic sine.

 

Polar equation: .

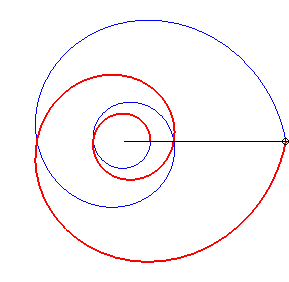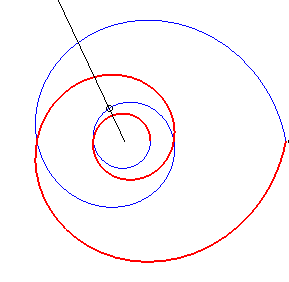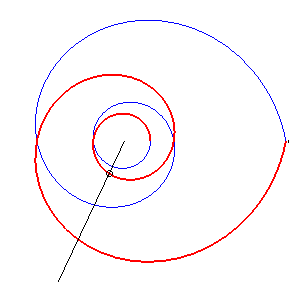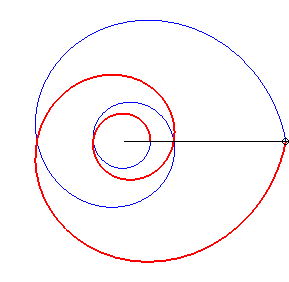
The rotating rod spiral is the trajectory of a massive ring sliding without friction on a horizontal rod in rotation around a centre when the ring goes to infinity. See on this website a derivation of the polar equation above.
 

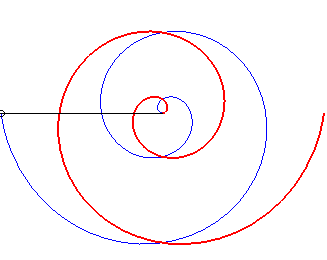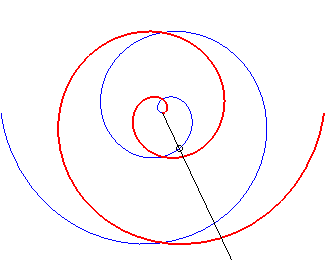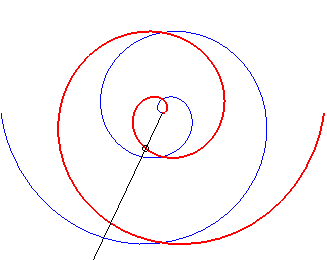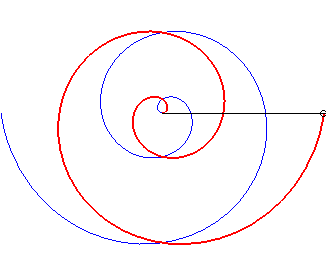
Case b =  a: the equation can be written .	Case b = – a: the equation can be written .	Case b = – 2a.

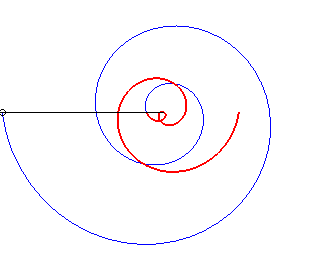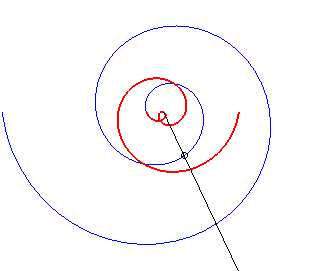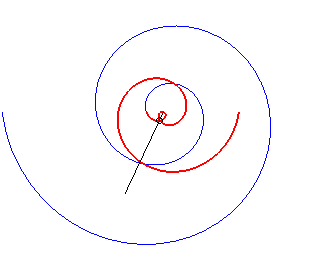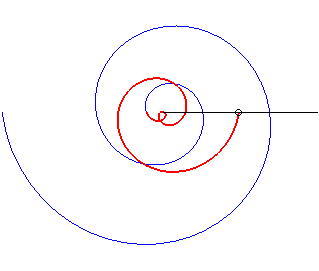Note that the curve is similar to the curve in the first case if ab > 0 because, then, , and it is similar to the curve in the second case if ab < 0, because, then, ; in all the cases where a and b are not zero, the spiral therefore has a symmetry axis, like the Archimedean spiral; but the two infinite branches have asymptotes: the logarithmic spirals.

After this website, there are also cases where the ring oscillate on the rod ; the curve is so an epitrochoid.

These spirals are inverses of Poinsot spirals.
See also the spiral of the hyperbolic tangent.
 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2022