ENSEMBLE DE MANDELBROT
Mandelbrot set, Mandelbrotmenge (oder Apfelmännchen)

| fractal suivant | fractal précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
ENSEMBLE DE MANDELBROT
Mandelbrot set, Mandelbrotmenge (oder Apfelmännchen)

| Benoît
Mandelbrot (1924 -2010) : mathématicien français.
Ensemble étudié par Benoît Mandelbrot en 1978 puis par A. Douady et J.H. Hubbard en 1982. Sites : fr.wikipedia.org/wiki/Ensemble_de_Mandelbrot et beaucoup plus complet en anglais : en.wikipedia.org/wiki/Mandelbrot_set john.bonobo.free.fr/fractal/doc.php?page=22 ftp.informatik.rwth-aachen.de/maple/mfrmand.htm mathematische-basteleien.de/apfelmaennchen.htm |
| Ensemble connexe d'aire évaluée à 1,50659... dont la frontière est de dimension fractale égale à 2. |
L'ensemble de Mandelbrot
est l'ensemble des complexes
c tels que la suite récurrente
définie par
soit bornée, autrement dit tels que 0 soit un "prisonnier" de la
fonction
définie par
,
ou encore que c appartienne à l'ensemble
de Julia rempli:
.
Une condition équivalente est que l'ensemble de Julia
soit connexe.
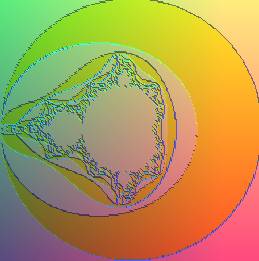
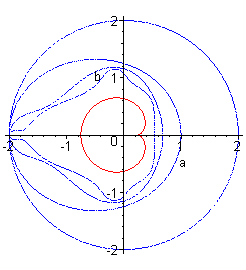
| On montre que si la suite La figure de gauche montre le tracé des courbes implicites La figure de droite, qui fait apparaître les 100 premiers domaines ci-dessus, a été obtenue comme suit : appelant "durée de vie" le premier entier n tel que |
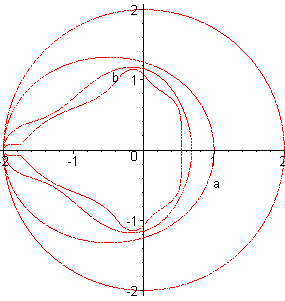 |
 |
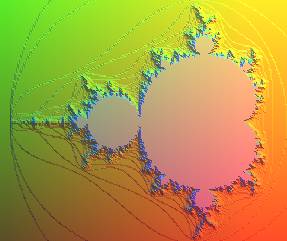
| On obtient une meilleure vision de l'ensemble de Mandelbrot
en représentant la fonction qui à c associe sa durée
de vie si celle-ci est inférieure à 100, et 100 sinon ; on
obtient une surface que l'on pourrait désigner par "plateau de Mandelbrot";
ce plateau, représentant D100 et
les contreforts qui y mènent, donne une bonne idée de l'ensemble
de Mandelbrot limite.
Si, comme à droite, on ne représente que D100, on perd certaines ramifications extrêmement fines de |
 |
 |
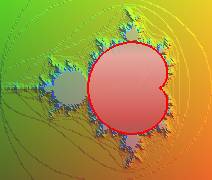
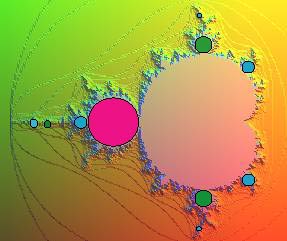
| La partie principale de Les ensembles de Julia correspondants sont des courbes fermées simples (mais fractales). D'après un théorème sur les fonctions complexes, l'intérieur de la cardioïde est l'ensemble des valeurs de c pour lesquelles la fonction Cet ensemble est donc formé des points c tels qu'il existe un z vérifiant Son intersection avec |
 |
 |
| On définit de même l'ensemble On conjecture que la réunion des Pour obtenir la frontière de |
 |
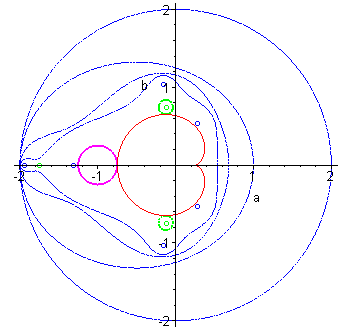 |
| D'autres points de Pour déterminer les points de Misiurewicz, on résout |
On peut définir plus généralement
un ensemble de Mandelbrot pour toute famille ()
de transformations du plan complexe comme étant l'ensemble des c
tels que la suite
,
où a est un point critique de
,
est bornée.
Quelques exemples ci-dessous (voir aussi cette
page):
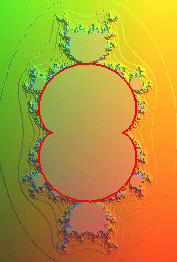 
Ensembles de Mandelbrot associé à |
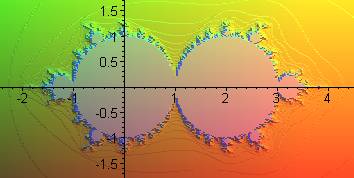 Ensemble de Mandelbrot pour |
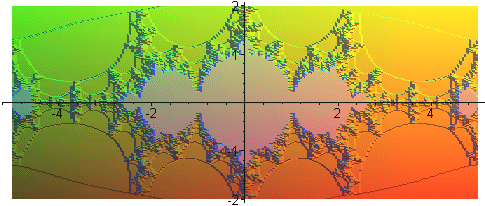 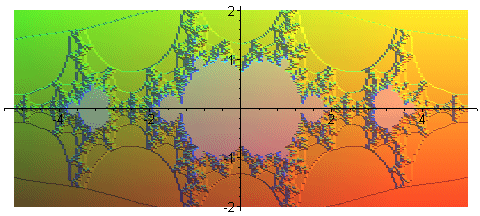
Ensembles de Mandelbrot pour |

Même les extra-terrestres connaissent l'ensemble de Mandelbrot
!
| fractal suivant | fractal précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2010