SAUCISSE DE MINKOWSKI
Minkowski Sausage, Minkowskische Wurst
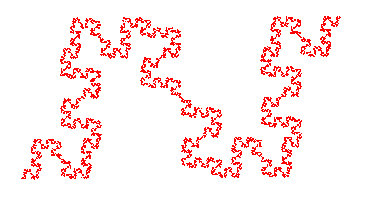
| fractal suivant | fractal précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
SAUCISSE DE MINKOWSKI
Minkowski Sausage, Minkowskische Wurst
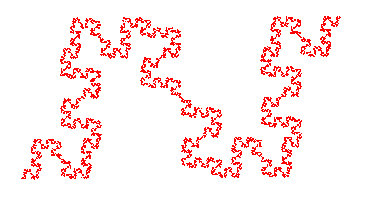
| Hermann Minkowski (1864 -1904) : mathématicien allemand. |
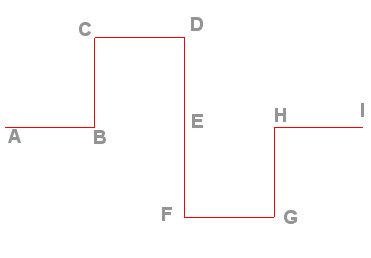
| La saucisse de Minkowski est l'attracteur
dans le plan des 8 similitudes de rapport 1/4 transformant (A, I)
successivement en (A, B), (B, C), (C, D) , (D, E), (E, F), (F, G), (G,
H), (H, I) (voir figure).
Sa dimension fractale est donc ln 8/ln 4 = 3/2. |
 |
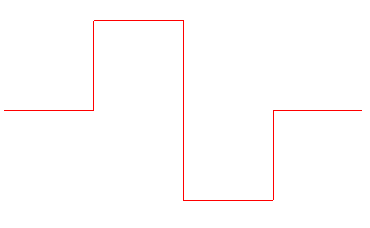
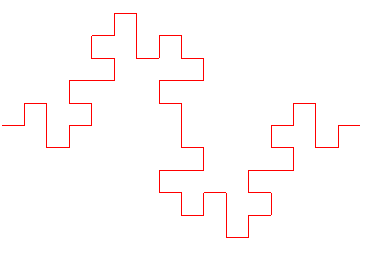
Voici la suite des
compacts convergeant vers cette courbe, en partant de [AI] :
 |
 |
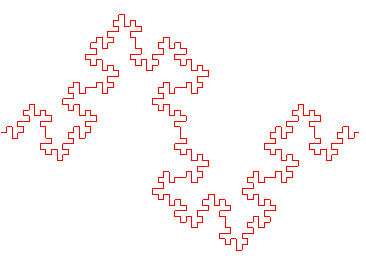 |
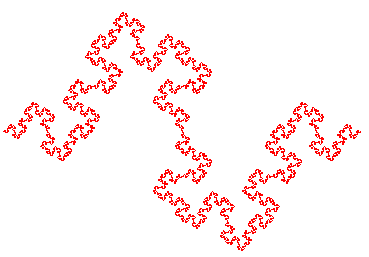 |
| Quatre saucisses de Minkowski dont les extrémités sont aux sommets d'un carré donnent l'île de Minkowski, parfois aussi dénommée "île de Koch quadratique". | 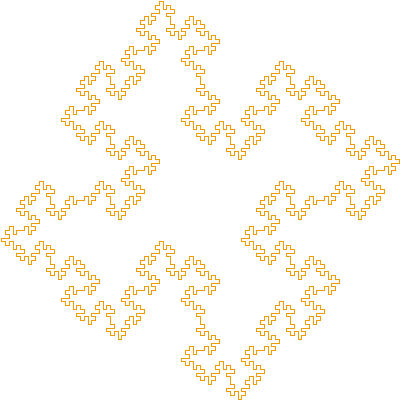 |
| fractal suivant | fractal précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2014